Булига Костянтин Борисович
кандидат технічних наук, доцент
Київський національний університет культури і мистецтв
місто Київ
Булига Олена Анатоліївна
Національний транспортний університет
місто Київ
Анотація: для многочленів Якобі, які є найбільш загальним випадком ортогональних многочленів, отримано нові рекурентні співвідношення, що включають різноманітні комбінації ортогональних многочленів і їх похідних. Як окремий випадок розглянуто ортогональні многочлени Лежандра.
Ключові слова: ортогональні многочлени Якобі, ортогональні многочлени Лежандра, рекурентні співвідношення, комбінації ортогональних многочленів і їх похідних, гама-функції Ейлера.
При реалізації чисельних методів виникає необхідність обчислення визначених інтегралів від виразів, що включають різні комбінації ортогональних многочленів і їх похідних. Рекурентні співвідношення і формули диференціювання, які є в літературі [1, 2], не дозволяють обчислювати інтеграли такого типу без значних витрат ручної праці. Нижче наводяться деякі нові співвідношення для многочленів Якобі, застосування яких дозволяє виконувати такі обчислення за допомогою ЕОМ.
Для цілих невід’ємних значень п прийнято [2]:
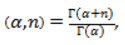
де Г ( α) - гама-функція Ейлера.
Тоді загальний вираз для довільного многочлена Якобі можна записати у вигляді
![]()
а співвідношення ортогональності
![]()
Розглянемо формулу вигляду
![]()
Покажемо, що коефіцієнти ![]() обчислюються за формулою
обчислюються за формулою
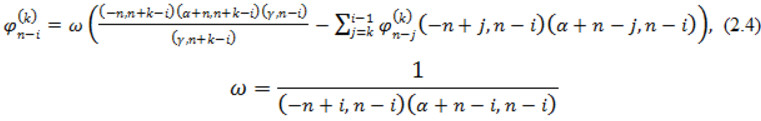
Розглянемо випадок k=1. Похідна за х від виразу (2.1) записується таким чином
![]()
а для многочленів, степінь яких менша за n, (2.1) записується у вигляді
![]()
Знаходячи відношення коефіцієнтів при рівних степенях х у виразах (2.5) і ![]() , приходимо до формули
, приходимо до формули
![]()
Аналогічно для k=2
![]()
Порівнюючи попередні формули, за індукцією отримаємо (2.4).
Співвідношення ортогональності для k-ї похідної від многочлена Якобі і довільного многочлена Якобі з урахуванням (2.3) приймає вигляд:
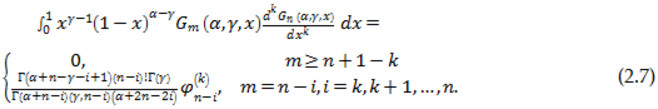
Розглянемо також вирази, які складаються з добутків многочленів Якобі і степеневих функцій.
![]()
де
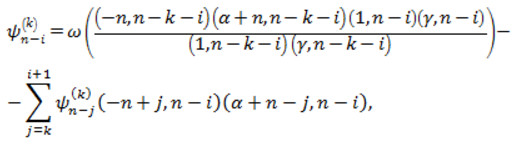
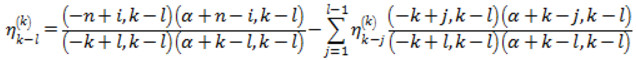
Формула (2.8) доводиться аналогічно формулі (2.3). співвідношення ортогональності в цьому випадку приймає вигляд
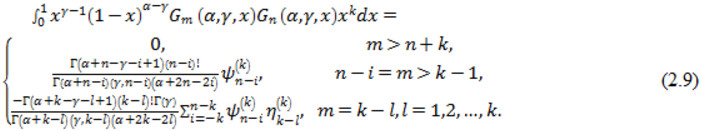
Розглянемо окремий випадок многочленів Якобі – многочлени Лежандра, які можна представити як
![]()
Для многочленів Лежандра співвідношення (2.7) приймає вигляд
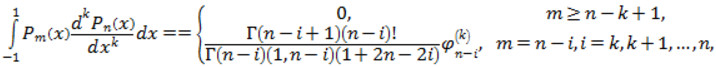
де
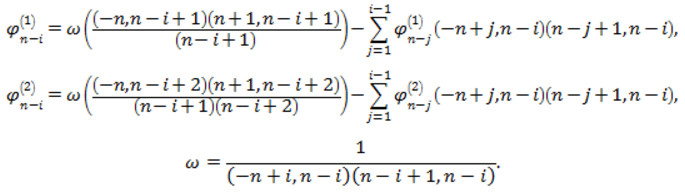
Враховуючи властивості гама-функції Ейлера
![]()
остаточно отримаємо
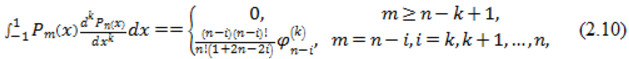
Співвідношення (2.10) приймає вигляд
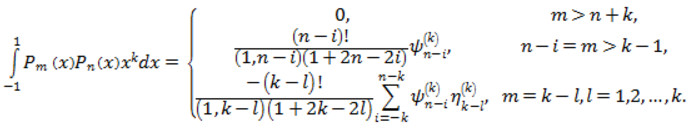
Враховуючи властивості гама-функції Ейлера остаточно отримаємо
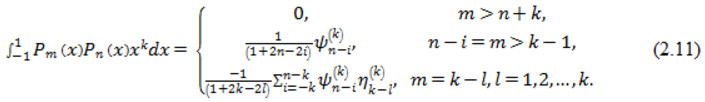
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Ортогональные многочлены. Материал из Википедии — свободной энциклопедии [Електронний ресурс] // Режим доступу: https://ru.wikipedia.org/wiki/%D0%9E%D1%80%D1%82%D0%BE%D0%B3%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D1%87%D0%BB%D0%B5%D0%BD%D1%8B
2. Суетин П.К. Классические ортогональные многочлены /П.К.Суетин – Москва: ФИЗМАТЛИТ, 2007. – 408 с.

