Шведова Вікторія Вікторівна

доцент, кандидат технічних наук,

Національний технічний університет України

«Київський політехнічний інститут імені Ігоря Сікорського,

м. Київ, Україна

 

 Анотація: Визначення характери розподілу похибок вимірювання часто є нелегкою процедурою, яка потребує постановки додаткових експериментів. Тому часто, за потребою врахування виду розподілу похибки вимірювання, використовують так звану «оцінку зверху», коли похибці приписують рівномірний розподіл. Однак при встановленні показника достовірності контролю, коли враховуються не лише межі похибки вимірювання, а й вид її розподілу оцінки цієї достовірності значно різняться в залежності від розподілу похибки вимірювання. В публікації показано яким чином доведений факт виду розподілу дозволяє підвищити оцінку достовірності контролю тим самим уникнувши невиправданого її заниження в наслідок неповної інформації та вибору «оцінок зверху».

 Ключові слова: похибка вимірювання, вид розподілу, достовірність контролю.

 

 Визначення характери розподілу похибок вимірювання часто є нелегкою процедурою, яка потребує постановки додаткових експериментів. Тому часто, за потребою врахування виду розподілу похибки вимірювання, використовують так звану «оцінку зверху», коли похибці приписують рівномірний розподіл. Однак при встановленні показника достовірності контролю [1], коли враховуються не лише межі похибки вимірювання, а й вид її розподілу оцінки цієї достовірності значно різняться в залежності від розподілу похибки вимірювання. 

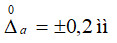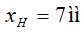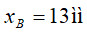 Вплив виду розподілу на достовірність контролю проілюструємо таким прикладом. Потрібно оцінити достовірність контролю діаметру деталі та ризики хибної та невизначеної відмови, якщо під час контролю наявна адитивна випадкова похибка  , а границі поля допуску становлять:  та . Розв’язати задачу для випадку а) розподіл контрольованого параметра та випадкової похибки рівномірні; б) розподіл контрольованого параметра рівномірний, а випадкової похибки – нормальний.

 Якщо для контрольованого параметра вибір рівномірної моделі розподілу є логічним, адже для практичних цілей придатним буде виріб з буд-яким значенням параметрам, що контролюють, аби він попадав у зазначені межі, то розподіл похибки засобу вимірювальної техніки, яким цей параметр вимірюють може бути різним.

 Отже вимірюваний параметр (діаметр деталі) має знаходитись в діапазоні:

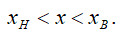
 Реальний результат вимірювання, що супроводжується випадковою похибкою:

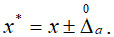
 Ймовірність хибної відмови (визнання контрольованої величини такою, що вийшла за границі зони допуску при дійсному входженні величини в зону допуску) визначається виразом [2]:

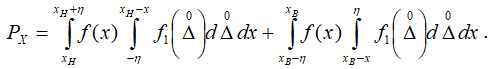
 Для рівномірного розподілу контрольованого параметра в зоні допуску маємо аналітичний вираз щільності розподілу: 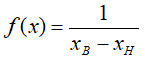 . Для рівномірного розподілу випадкової похибки маємо аналітичний вираз щільності розподілу:  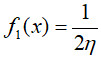. Тоді для рівномірних розподілів контрольованого параметра та випадкової похибки вимірювання ймовірність хибної відмови:

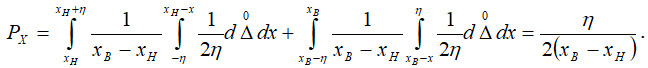
 З огляду на умову задачі для рівномірного розподілу контрольованого параметра в зоні допуску маємо аналітичний вираз щільності розподілу:

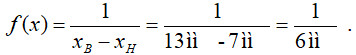
 Для рівномірного розподілу випадкової похибки маємо аналітичний вираз щільності розподілу: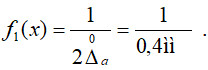  

 Тоді для рівномірних розподілів контрольованого параметра та випадкової похибки вимірювання:

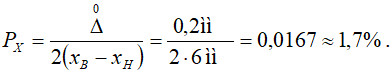
 Аналогічно попередньому ймовірність невизначеної відмови [2]:

 

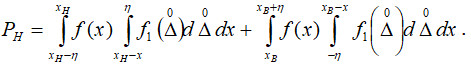
 Тоді

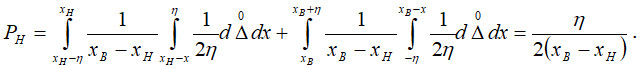
 Тоді для умови задачі для рівномірних розподілів контрольованого параметра та випадкової похибки вимірювання:

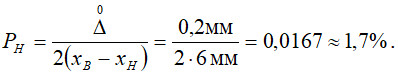
 Отже достовірність прийняття правильного рішення щодо стану контрольованого об’єкта (в нашому випадку діаметра втулки) буде визначатись і дорівнювати:

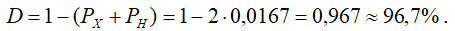
 Для нормального ж розподілу випадкової похибки маємо аналітичний вираз щільності розподілу: 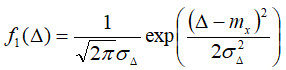 . Математичне сподівання випадкової похибки дорівнює нулю:  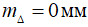(за умови симетричної похибки засобу вимірювання, що частіше зустрічається на практиці). Оцінку стандартного відхилення можна отримати за співвідношенням  .

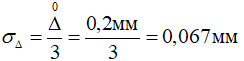 Тоді ймовірність хибної відмови:

 

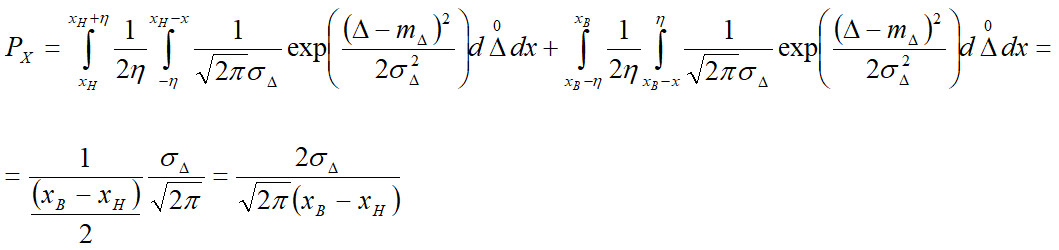
 Аналогічно попередньому ймовірність невизначеної відмови:

 

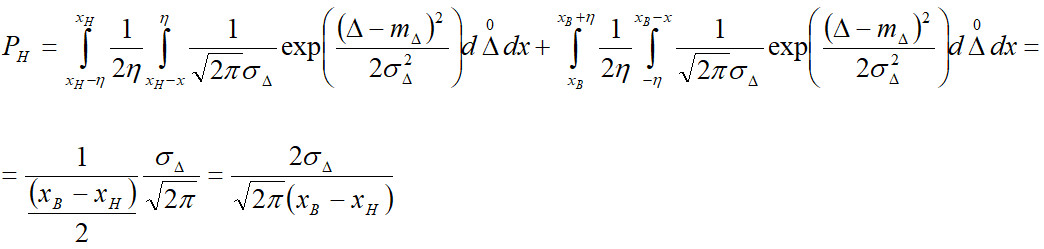
Для умови задачі маємо:

• ймовірність хибної відмови 

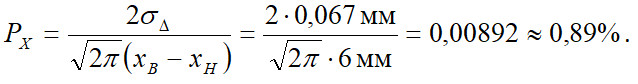
• ймовірність невизначеної відмови

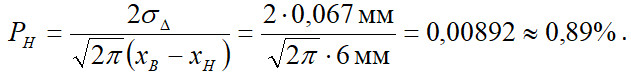
• достовірність контролю

 Отже порівнюючи отримані вирази маємо, що для випадку рівномірного розподілу похибки вимірювання достовірність контролю становить  , а для нормального -  , що є суттєвим враховуючи той факт, що прийнятні рівні достовірносте для багатьох практичних задач починаються з   [3].

 Аналітично порівняти «виграш» від заміни рівномірного розподілу нормальним можна отримати з виразу:

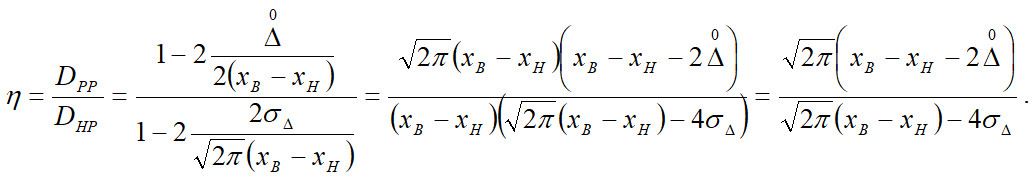
 де   - достовірність за умови рівномірного розподілу похибки вимірювання контрольованого параметра;  - достовірність за умови нормального розподілу похибки вимірювання контрольованого параметра;

 Звісно, що безпідставно замінювати форму розподілу похибки вимірювання ми не маємо право. Однак провівши дослідження виду розподілу похибки вимірювання з використанням одного з відповідних ситуації вимірювання критеріїв перевірки можна отримати суттєве підвищення рівня достовірності лише за рахунок відмови від використання завищених оцінок, скориставшись науково обґрунтованим підходом.

 

Література:

1. Шведова В.В. Алгоритмічне забезпечення системи контролю параметрів продукції // Збірник статей учасників шостої Міжнародної практично-пізнавальної конференції «Наукова думка сучасності і майбутнього», м. Дніпро 2016 (23-30 листопада 2016) – С. 11-13.

2. Володарський Є.Т., Кухарчук В.В., Поджаренко В.О., Сердюк Г.Б. В 68 Метрологічне забезпечення вимірювань і контролю. Навчальний посібник. - Вінниця: ВДТУ, 2001. –219с.

3. Шведова В.В., Бокеєва В.В. Дослідження впливу випадкової адитивної похибки засобу вимірювання на достовірність контролю продукції //Збірник статей учасників двадцятої всеукраїнської практично-пізнавальної конференції «Наукова думка сучасності і майбутнього», м. Дніпро 2018. – С. 70 - 73.