Федорчак Олексій Євстахійович,

к.е.н., асистент кафедри підприємництва та екологічної експертизи товарів,

Національний університет «Львівська політехніка», м. Львів

  Анотація. Проаналізовано наукову література за проблематикою формування інвестиційних портфелів із банківських металів. Виявлено, що ця проблема висвітлена недостатньо на прикладному рівні, оскільки пропонована структура такого портфеля, розрахована на основі фактичних даних, не була опублікована. Представлено статистичний аналіз динаміки вартості банківських металів. Обчислено структура оптимального інвестиційного портфеля із цих металів. Статистично доведено, що деякі види банківських металів слід виключати з метою отримання портфеля із найкращим співвідношенням дохідності та ризику.

  Ключові слова: інвестиції, банківські метали, інвестиційний портфель, дохідність, ризик.

  Методи дослідження. Політична та економічна нестабільність в Україні зумовлюють необхідність пошуку засобів збереження та примноження капіталу на основі вибору надійних довгострокових об’єктів для інвестування. Одним із таких напрямків є ринок банківських металів, на якому можна придбати або продати золото, срібло, платину та паладій. Вартість цих металів, як буде показано нижче, помітно виросла за останні 5 років, в той час як темпи інфляції уповільнились, що дає змогу будувати стратегію не тільки збереження капіталу від знецінення, але й для його примноження. Основою для формування такої стратегії є інвестиційний портфель, розрахований із використання статистичного аналізу ризику та дохідності, та який базується на обчислення структурних коефіцієнтів. 

  Вперше ідея щодо формування інвестиційних портфелів на основі застосування виключно математичних засобів була опублікована американським економістом Г. Марковіцом[1]. Геніальність пропонованого рішення полягала у тому, що структуру інвестиційного портфеля можна розрахувати на основі математичної оптимізаційної задачі, яка шляхом доповнення добутками Лагранжа може бути розв’язана методом Гаусса,методом Крамера або матричним методом. Цю задачу можна представити наступним чином:

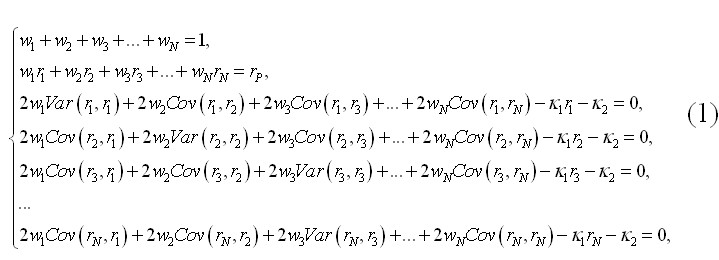
  де    - частки інвестиційних у загальній структурі портфеля, част. од.;    - дохідність кожного активу у портфелі, част. од.;  r_P - прийнятний або середні рівень дохідності портфеля, част. од.; V_ar - варіація дохідностей інвестиційних активів; C_ov - коваріація інвестиційних активів; N - кількість активів у портфелі; k₁ , k₂  - добутки Лагранжа, випадкові числа, які не відіграють жодної ролі і необхідні тільки для того, щоб звести системи лінійних рівнянь до однорідної форми.

  Хоча розв’язання задачі видається складним, проте на практиці це можливо, шляхом зведення її до матричного рівняння та використання матричного методу:

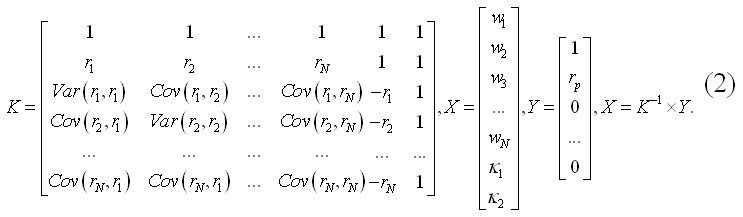
  Таким чином, на основі зведення оптимізаційної задачі Марковіца до лінійного однорідного рівняння можна розрахувати оптимальну структуру інвестиційного портфелю, ля якої спостерігатиметься середня дохідність із можливих та найнижчий рівень ризику.

  Результати дослідження. Представлені вище математичні засоби можна використати для визначення оптимальної структури інвестиційного портфеля, який складається зі банківських металів. На основі даних порталу Finance.ua зібрано інформацію про місячні ціни на золото, срібло, платину та паладій за період з 01.12.2012 по 01.10.2017 рр. (табл. 1).

Таблиця 1

Динаміка вартості золота, срібла, платини та паладію за період з 01.12.2012 по 01.10.2017 рр., грн./10 тройських унцій

  Примітка: побудовано на основі [2]

  Використання ретроспективних даних по динамці курсу банківських металів на основі моделі (1) слід розпочати із розрахунку дохідності (рис. 1). На основі цього можливим є обчислити коваріаційну матрицю та записати модель (1) у матричній формі (2).

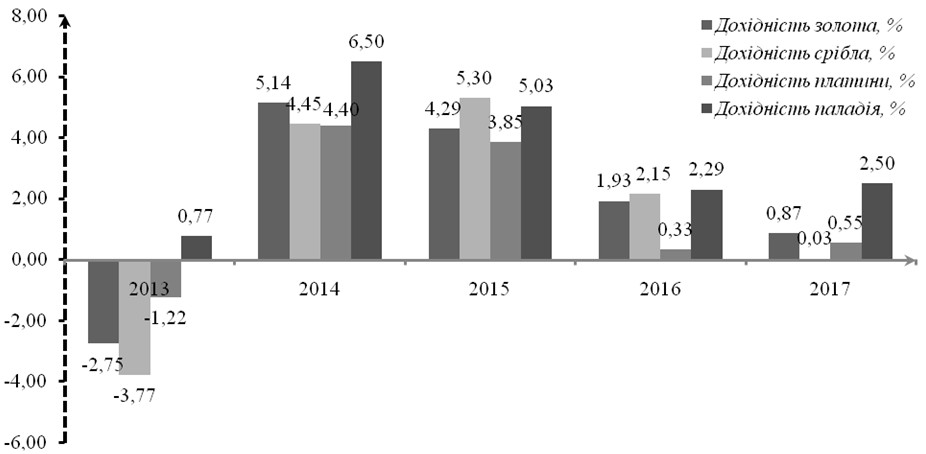
 Рис. 1. Динаміка річного середнього арифметичного помісячної дохідності банківських металів за період з 2013 по 2017 рр.

  Примітка: у 2017 р. враховано 9-ть повних місяців, зі січня по вересень.

  На основі значень помісячної дохідності банківських металів протягом останніх 5-ти років розраховано коваріаційну матрицю (табл. 2).

Таблиця 2

Коварціаційна матриця помісячних дохідностей банківських металів за період з 01.12.2013 по 01.10.2017 р.

Наступним етапом розрахунку оптимальної структури досліджуваного інвестиційного портфеля є вибір дохідності. Чим ближчим є цей параметр до середнього арифметичного дохідностей активів портфеля, тим більша ймовірність, що розв’язок системи рівнянь (1) буде відповідати вимогам до структурних коефіцієнтів. Тому для початку приймаємо рівень дохідності рівним 2,48 % на місяць, що є середнім значенням помісячних дохідностей золота, срібла, платини та паладію на вітчизняному ринку банківських металів за період з 2013 по 2017 рр. Запишемо модель (2) із врахуванням представлених вище даних:

  Як бачимо, в результатів розрахунків, доведено, що на основі чотирьох досліджуваних активів, якщо брати за основу помісячні дохідності за період з 2013 по 2017 рр., неможливо сформувати оптимальний інвестиційний портфель, використовуючи модель (2). Проте можливим є виключення найбільш проблемного активу - срібла, оскільки для нього, структурний коефіцієнт є найменшим. Провівши розрахунки для портфеля, який складається із золота, платини та паладію отримано таку структуру:

  Цей портфель базується на середній помісячній дохідності 2,48 %. Метод підбору значень одержано, що можливим є портфель із двох активів та помісячною дохідністю 2,8 %:

  На основі одержаних структурних коефіцієнтів розрахуємо зміну ризику (на основі середньоквадратичного відхилення дохідностей) для обох портфелів. Для портфеля із трьох активів середній ризику рівний 12,1 %, для портфеля із двох активів - 12,8%. Тобто, зміна ризику виключенні платини із портфеля рівна 5,3%, а зміна дохідності рівна 12,9 %. Це говорить про те, що у інвестиційний портфеля із банківських металів слід включити золота та паладій, причому частка золота має бути рівна 55,4 %, а паладію - 44,6 %.

Література:

1. Markowitz, H.M. (March 1952). "Portfolio Selection". The Journal of Finance. 7(1): 77–91.

2. Курс банківських металів НБУ / Інтернет-видання «Finance.ua». - режим доступу: https://tables.finance.ua/ru/metals/official.