Шатохин Владимир Михайлович,

профессор, доктор технических наук,

Национальный университет строительства и архитектуры,

Украина, Харьков

 

Шаповалов Александр Васильевич,

доцент, кандидат технических наук,

Национальный фармацевтический университет,

Украина, Харьков

 

Кутовая Ольга Вячеславовна, доцент,

кандидат технических наук,

Национальный фармацевтический университет,

Украина, Харьков

 

  В статье предлагается новый подход по созданию экономичного универсального алгоритма расчета нелинейных колебаний произвольных цепных дискретных систем в рамках метода гармонической линеаризации. В его основе лежит представление уравнений движения с помощью импульсно-частотных характеристик (ИЧХ) в интегральной форме. Число нелинейных интегральных уравнений оказывается в этом случае равным числу нелинейностей и не зависит от размерности линейных контуров модели.

 

  Ключевые слова: нелинейные колебания, импульсно-частотные характеристики, амплитуда деформаций, нелинейные модели, жесткость нелинейного соединения.

 

  При исследовании установившихся колебаний в нелинейных моделях механических систем хорошо зарекомендовал себя метод гармонической линеаризации. В предположении, что при гармоническом возмущении изменения обобщенных координат носят характер, близкий к гармоническому, осуществляется линеаризация модели и решение задачи сводится к решению систем нелинейных уравнений. Трудоемкость задачи существенно зависит от порядка системы, что всегда делает целесообразным его уменьшение. Особую актуальность этот вопрос приобретает в оптимизационных задачах. Так как в большинстве практических задач, например, при исследовании динамики машинных агрегатов с ДВС, число нелинейностей существенно меньше размерности линейных контуров, то в указанной системе уравнений большая их часть оказывается линейными. С учетом сказанного, естественным в этом случае оказывается прием последовательного исключения линейных уравнений. Алгоритмы редукции ориентированы на простые цепные системы с одним нелинейным соединением. 

  В ряде работ [1, 2, 3], посвященных динамическому синтезу силовых передач машин с нелинейным силиконовым демпфером, при решении задачи анализа использовался алгоритм расчета вынужденных колебаний, основанный на методе редукции масс системы, предложенном И. Ш. Нейманом [4]. Алгоритм является достаточно быстродействующим, так как позволяет свести решение задачи о вынужденных колебаниях нелинейной многомассовой системы к задаче о вынужденных колебаниях эквивалентной двухмассовой системы. Это обстоятельство и обусловило применение его в задачах оптимизации, требующих многократного решения задачи анализа. Однако при использовании процедуры редукции не удается автоматически настроить алгоритм на решение задачи анализа дискретной системы произвольной структуры с несколькими нелинейностями, что, естественно, сужает границы его применения.

  Предложен новый подход по созданию экономичного универсального алгоритма расчета нелинейных колебаний произвольных цепных дискретных систем в рамках метода гармонической линеаризации. В его основе лежит представление уравнений движения с помощью импульсно-частотных характеристик (ИЧХ) в интегральной форме [5]. Число нелинейных интегральных уравнений оказывается в этом случае равным числу нелинейностей и не зависит от размерности линейных контуров модели.

  Уравнения движения записываются в виде

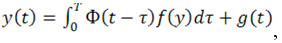
  где 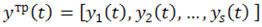   – вектор деформаций нелинейных соединений (тр – знак транспонирования); 

  Т – период колебаний;

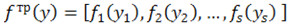    – нелинейная вектор-функция, причем   ;

 

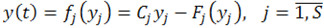
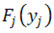 – нелинейная характеристика j-го нелинейного соединения;

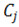   и 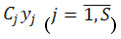   – коэффициент жесткости и линейная часть упругого момента в j-м нелинейном соединении;

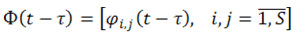 – матрица ИЧХ линеаризованной модели, у которой нелинейные соединения заменены линейными с коэффициентом жесткости  , 

 ;

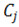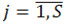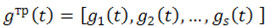  – вектор-функция реакций линеаризованных нелинейных соединений на внешнее возмущение ( в рассматриваемом случае – гармоническая функция.

  Как и при традиционном подходе, предполагается, что решения нелинейных интегральных уравнений при моногармоническом возмущении с достаточной точностью описываются выражениями

 ,

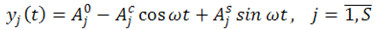  где 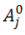 – средняя деформация,  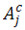,  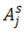 – соответственно косинусная и синусная амплитуды основной гармоники деформации j-го нелинейного соединения.

  С учетом этого, представляя ИЧХ и нелинейные функции соответствующими рядами Фурье, удалось показать, что решение системы нелинейных интегральных уравнений может осуществляться по следующему алгоритму.

  Задаются начальные значения амплитуд деформаций нелинейных соединений 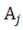 ,  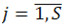. По ним с помощью уравнений

 

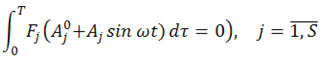
  определяются средние деформации 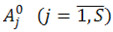  , а затем с помощью формул

  ,

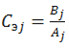 Где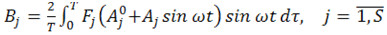   

  определяются эквивалентные жесткости.

  После этого решается система линейных алгебраических уравнений

 ,

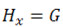  где

 

  а элементы матрицы Н выражаются через 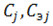  и основные гармоники ИЧХ (их нахождение не требует специального алгоритма построения ИЧХ) и определяются  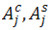, а, следовательно, и новые амплитуды 

 

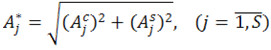
  Задача будет решена, если указанные амплитуды окажутся одинаковыми (на практике отличающимися на малую заданную величину). Это удобно сделать, организовав поиск минимума функции невязки

 

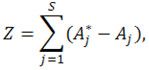
  число переменной которой равно числу нелинейностей. Принципиальным является то, при каждом вычислении функции невязки необходимо решать систему линейных алгебраических уравнений порядка 2s, а при традиционном подходе – порядка 2n, где n – число обобщенных координат.

  Разработаны рациональные приемы реализации отдельных этапов предлагаемого алгоритма:

- получение основных гармоник ИЧХ без специального алгоритма;

- нахождение указанных гармоник ИЧХ, элементов вектора G и амплитуд колебаний каждой массы на данной частоте с использованием только одного разложения матрицы системы линейных алгебраических уравнений порядка 2n на две треугольные;

- нахождение нулевого минимума функции невязки;

- использование простых приближенных формул для определения средней деформации и эквивалентной жесткости нелинейного соединения.

Рассмотренный алгоритм был использован для расчета вынужденных колебаний в многомассовой модели машинного агрегата с ДВС.

 

Литература:

1. Оптимизация крутильных систем с силиконовым демпфером./В.Н. Карабан, А.В. Шаповалов, В.М. Шатохин и др. //Динамика и прочность машин.1981. Вып. 34. С. 89-93.

2. Шаповалов А.В. Об эффективности алгоритма динамического синтеза, основанного на методе инвариантных точек. // Динамика и прочность машин.1987. Вып. 45. С. 58-61.

3. Шаповалов А.В., Шатохин В.М. Об алгоритме расчета оптимальной вязкости силиконового масла в демпфере крутильных колебаний. //Динамика и прочность машин.1987. Вып. 46. С. 72-74.

4. Нейман И.Ш. Крутильные колебания многомассовых нелинейных систем. – М.: Оборон-из,1947. – 132 с.

5. Шатохин В.М., Штейнвольф Л.И. О построении обобщенных импульсно-частотных характеристик механических систем. // Динамика и прочность машин.1988. Вып. 48. С. 88-93.