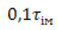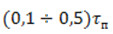Булига Костянтин Борисович
кандидат технічних наук, доцент
Київський національний університет культури і мистецтв
місто Київ
Булига Олена Анатоліївна
Національний транспортний університет
місто Київ
Анотація: За допомогою регіонально-проекційного метода розв’язана задача визначення температурного поля поверхні лазерного дзеркала під дією імпульсного нагріву. Наведена таблиця варіантів розрахунку та розподіл температури зі зміною часу.
Ключові слова: поверхнева плівка, тепловий потік, імпульсний нагрів.
Одновимірне нестаціонарне температурне поле в поверхневій плівці під дією теплового потоку інтенсивністю q підкоряється рівнянню
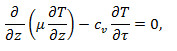
де 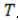 - розподіл температури,
- розподіл температури,
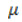 - коефіцієнт теплопровідності,
- коефіцієнт теплопровідності,
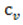 - об’ємна теплоємність,
- об’ємна теплоємність,
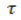 – час,
– час,
і граничним умовам 3-го і 2-го типів на нижній і верхній поверхнях плівки.
Застосовуючи загальну процедуру регіонально-проекційного метода [1], отримаємо інтегральне співвідношення
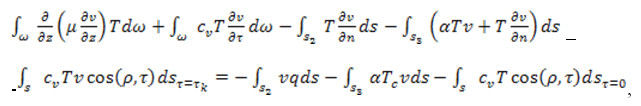
де 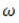 – часово-просторова область,
– часово-просторова область,
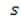 – поверхня області,
– поверхня області,
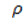 – нормаль до поверхні,
– нормаль до поверхні,
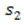 – ділянка поверхні, на якій задана гранична умова 2-го роду,
– ділянка поверхні, на якій задана гранична умова 2-го роду,
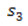 – ділянка поверхні, на якій задана гранична умова 3-го роду,
– ділянка поверхні, на якій задана гранична умова 3-го роду,
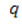 – інтенсивність теплового потоку.
– інтенсивність теплового потоку.
Далі застосовується алгоритм методу:
1) плівка ділиться на декілька шарів, у загальному випадку різної товщини,
2) в кожному шарі інтегральне співвідношення заміняється квадратурними формулами, що дає змогу перейти до дискретної множини точок, температура в яких є шуканими невідомими,
3) розв’язуючи отриману систему лінійних алгебраїчних рівнянь, отримаємо дискретну множину значень температури в точках плівки.
Розглянемо приклад. Поверхнева плівка товщиною 0,5 мм піддається періодичній дії теплового потоку інтенсивністю q=1900000 Вт/м 2, час дії імпульсу 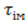 =4•10 -5 сек, час паузи
=4•10 -5 сек, час паузи 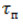 =4,96•10 -3 сек, початкова температура плівки 20 0 С. З оберненої сторони плівки задана гранична умова 3-го роду при коефіцієнті обміну α = 104 і температурі середовища 20 0С. Коефіцієнт теплопровідності матеріалу дорівнює 179 Вт/(м•к), об’ємна теплоємність 3,73•10 6 дж/(м 3 •к).
=4,96•10 -3 сек, початкова температура плівки 20 0 С. З оберненої сторони плівки задана гранична умова 3-го роду при коефіцієнті обміну α = 104 і температурі середовища 20 0С. Коефіцієнт теплопровідності матеріалу дорівнює 179 Вт/(м•к), об’ємна теплоємність 3,73•10 6 дж/(м 3 •к).
Для розв’язання задачі використано регіонально-проекційний метод [1]. Приймаючи верхню поверхню плівки за початок координат, її розділено по висоті на 19 ділянок точками з координатами (мм): 0,0; 0,05; 0,078125; 0,10625; 0,13438; 0,1625; 0,2047; 0,24688; 0,28906; 0,33125; 0,37344; 0,41563; 0,44375; 0,4625; 0,475; 0,48; 0,485; 0,49; 0,495; 0,5. У таблиці 1 наведені основні характеристики 4-х варіантів розрахунку, які отримано для 5 імпульсів.
Таблиця 1.
|
№ варіанта |
Інтенсивність теплового потоку |
Кількість кроків за часом |
Крок за часом |
Температура поверхні |
||
|
Імпульс |
Пауза |
В кінці 1-го імпульсу |
В кінці 5-го імпульсу |
|||
|
1 |
q |
10 |
|
|
20,462 |
20,600 |
|
2 |
10q |
10 |
|
|
24,612 |
26,221 |
|
3 |
10q |
55 |
|
|
25,136 |
25,616 |
|
4 |
10q |
105 |
|
|
25,136 |
26,693 |
На рисунку 1 показано зміну температури поверхні в 4-му варіанті розрахунків.
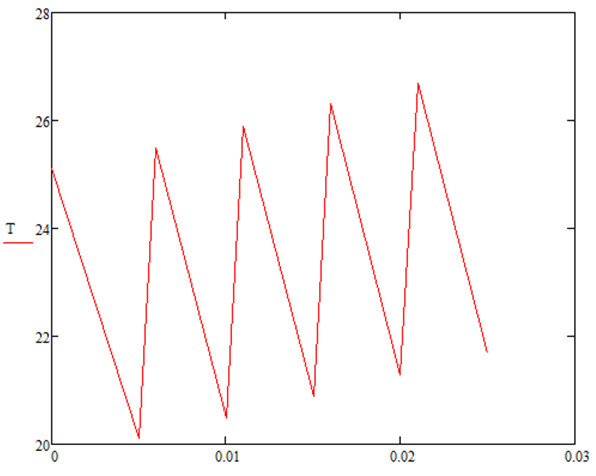
Рис.1.
Література:
1. Булига К.Б. О напряженно - деформированном состоянии тел вращения сложной формы при нестационарном температурном воздействии / К.Б.Булига, Б.М.Лисицын, О.Г.Мартынюк . – Прикладная механика, XXVIII, № 3, 1992, c. 71 - 76.