Босенко Дмитро Володимирович,

Національний технічний університет України «Київський політехнічний інститут імені Ігоря Сікорського»,

аспірант першого року навчання

 

Шмідт Богдан Сергійович,

Національний технічний університет України «Київський політехнічний інститут імені Ігоря Сікорського»,

магістр

 

Шведова Вікторія Вікторівна

Національний технічний університет України «Київський політехнічний інститут імені Ігоря Сікорського»,

к.т.н., доцент

 

 Анотація: в статті запропоновано послідовний алгоритм прийняття формування інтегрованої оцінки якості системи дистанційного навчання на основі експертного оцінювання.

 Ключові слова: система дистанційного навчання, експертне оцінювання, алгоритмічне забезпечення опрацювання експертних даних.

 

 При виборі найкращої для певних цілей системи дистанційного навчання вона оцінюється за певним переліком критерієм. При цьому не завжди характеристики критеріїв можуть бути отримані за об’єктивними вимірювальними процедурами. Часто для такої задачі залучаються кваліфіковані експерти. При цьому, як правило, градація можливих оцінок експертів представлена в лінгвістичні шкалі.

 В нашому випадку розглядаємо 4-х рівневу лінгвістичну шкалу: А, В, F, E, смислову відповідність яких можна представити таблицею.

Таблиця 1. 

 

 Зазвичай система дистанційного навчання має ряд критерії: надійність, валідність, зручні, якість інтерфейсу тощо. В нашому випадку їх 10. Кожний з експертів виставляє за кожний з 10-ти критерії лінгвістичну оцінку.

 Для застосування запропонованого алгоритму потрібно перевести лінгвістичні оцінки в числову шкалу. Пропонуємо обрати нелінійну шкалу, яку найчастіше використовують для оцінювання студентів у закладах вищої освіти – таблиця 2.

Таблиця 2.

 

 Якщо експертів декілька, то відповідно вони можуть виставити різні оцінки за різні критерії. Тому подальшим завданням є перевірка узгодженості оцінок експертів, в залежності від чого обирається спосіб поєднання оцінок окремих експертів.

 Нехай вихідна матриця результатів оцінювання трьома експертами має вигляд як в таблиці 3.

Таблиця 3.

 

 З таблиці видно, що оцінки експертів за критеріями 1, 3 7 та 9 абсолютно узгоджені, оцінки за критеріями 2, 6, та 8 скоріше узгоджені, оскільки по дві оцінки співпадають, а одна з оцінок дещо вища (критерій 2) або дещо нижча (критерії 6 та 8) порівняно з двома іншими.

 Для проведення розрахунків переведемо оцінки таблиці 3 у числовий вимір. Отримуємо таблицю 4.

 Таблиця 4.

 

 Традиційним на сьогодні способом перевірки узгодженості значень або виявлення аномальних результатів (або промахів) є критерій Грабса [1]. Вимогою застосування критерію Грабса є нормальність досліджуваної вибірки, але часто цей факт не перевіряють (ососбливо, якщо вибірка мала) і вважають, що вона належить нормальній генеральній сукупності. Другим за поширенням після критерію Грабса є критерій Ірвіна, яких дозволяє опрацьовувати вибірки різних розподілів. Перевірка за цими двома критеріями показала, що вони не є ефективними для виявлення узгодженості результатів експертного оцінювання, оскільки не виявляли очевидні промахи в оцінюванні.

Тому для виявлення оцінок, які є неузгодженими з усією вибіркою застосовано критерій Діксона [2]. За цим критерієм для вибірки з   елементів маємо розрахувати – таблиця 5.

Таблиця 5.

 

 

 Для критерія (характеристики) дистанційного курсу №5, оцінки з якого очевидно не узгоджені маємо: 

 

 Впорядковуємо вибірку: 

  

 Перевіряємо менший результат 0,6 за таблицею критичних значень для критерія Діксона:

 

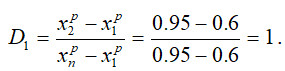
 Таблиця 6. Критеріальні значення коефіцієнтів Діксона (для прийнятого рівня значущості α).

 

 

 Для всіх рівнів довіри, наведених в таблиці результат 0,6 є промахом, оскільки .

 Перевіримо для критерію № 4 за критеріє Діксона

 

  

 Впорядковуємо вибірку

 

 Перевіряємо менший результат 0,65:

 

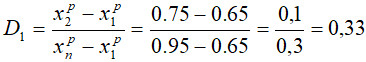
 Перевіряємо менший результат 0,95:

 

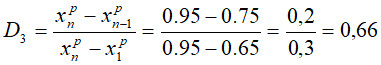
 Для всіх рівнів довіри, наведених в таблиці результат значення 0,65 та 0,95 не є промахом, оскільки   та .

 Отже даний критерій виявився ефективним для виявлення аномального результату у вибірці оцінювання.

 Перевіривши за критерієм Діксона усі критерії якості системи дистанційного навчання отримуємо таблицю виду 7 .

Таблиця 7. 

 

 Для отримання інтегрованої оцінки за кожним критерієм якості використовуємо алгоритм.

 Для узгоджених оцінок розраховувати середнє арифметичне, а для неузгоджених – медіану ряду.

 Тоді для нашого прикладу для критерія №2 (з узгодженими оцінками експертів) маємо:

 

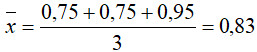
 а для критерію №5 (з неузгодженими оцінками експертів):

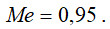
 В певній мірі такий результат може свідчити, про неврахування думки третього експерта (тобто вирішує переважна більшість). Дійсно оцінка медіани є менш точною ніж середнє арифметичне. Однак при високих оцінках двох інших експертів, оцінка третього може бути дещо не об’єктивною. Однак при збільшенні кількості експертів – до 4, 5 точність медіани збільшується.

 Далі прораховуємо інтегровані оцінки для кожного критерію – таблиця 8.

Таблиця 8. 

  

 Далі отриману числову оцінку переводимо за необхідності в лінгвістичний кортеж, за правилом:

Таблиця 9. 

 

 Отже в роботі запропоновано алгоритмічне забезпечення визначення інтегрованої експертної оцінки, зокрема,  системи дистанційного навчання, яке складається з трьох етапів: переведення експертних оцінок з лінгвістичної шкали в числову, перевірка узгодженості оцінок експертів, поєднання оцінок в залежності від результату попереднього етапу, що дозволяє отримати інтегровану оцінку якості критерії системи дистанційного навчання. В подальшому ці оцінки можуть бити використані для порівняння різних систем дистанційного навчання за сукупністю критеріїв.

 

Література

1. ДСТУ ГОСТ ИСО 5725-2:2005 Точність (правильність і прецизійність) методів та результатів вимірювання. Частина 2. Основний метод визначення повторюваності та відтворюваності стандартного методу вимірювань.

2. Третьяк Л.Н. Обработка результатов наблюдений: Учебное пособие. – Оренбург: ГОУ ОГУ, 2004. – 171 с.

3. Шмідт Б.С., Басенко Д.В., Шведова В.В. Аналіз методів кваліметричних вимірювань на основі експертного оцінювання і їх застосування для вирішення конкретної задачі педагогічного вимірювання // Збірник матеріалів ХVI Науково-практичної конференції студентів, аспірантів та молодих вчених «Ефективність та автоматизація інженерних рішень у приладобудуванні», м.Київ, 8-9 грудня 2020.