Третяк Татьяна Леонидовна
старший преподаватель
Национальный технический университет «Харьковский политехнический институт»
Украина, Харьков
Гуцаленко Юрий Григорьевич
старший научный сотрудник
Национальный технический университет «Харьковский политехнический институт»
Украина, Харьков
Мироненко Сергей Александрович
студент
Национальный технический университет «Харьковский политехнический институт»
Украина, Харьков
Аннотация: задача данной работы – с позиций представления об истории привлечения и обобщающих возможностях унифицированных многопараметрических отображений аффинного пространства в теории сложных криволинейных поверхностей рассмотрены способы формообразования зубчатых колес для усовершенствованных двухпараметрических передач с постоянным нормальным шагом.
Ключевые слова: многопараметрические отображения, зубчатые колеса, постоянный нормальный шаг, способы формообразования, точность.
Явление Украины во всемирной истории выдающихся разработок теории и практики зубчатых зацеплений связывается с последней четвертью XIX века, а именно с защитой в Новороссийском университете на тот момент житомиряниным Х. И. Гофманом магистерской диссертации по механике на тему «Теория зацеплений, обобщенная и развитая путем анализа» [1]. В этом труде разработана аналитическая форма произвольных зубчатых колес и основы современной аналитической теории зацеплений, созданы инженерные методы расчета и проектирования зубчатых зацеплений, разработаны новые виды зацеплений, теории кинематических пар и цепей, исследованы структуры и выведены общие уравнения механизмов, впервые классифицированных на основе объективных признаков, которые определяются уровнями структуры и движениями.
Во второй половине XX века вызовы развития авиационно-космического, атомно-энергетического машиностроения, оборонной промышленности, в том числе в части компактных зубчатых передач и вариаторов для бронетанковой и перспективной техники гражданского назначения, особенно актуализировали теоретические исследования в направлении обобщенной математизации формообразования криволинейных поверхностей зубчатых звеньев передаточных механизмов, поиска и синтеза на этой основе принципиально новых технических решений, обеспечивающих технико-экономическое превосходство разработок в условиях геополитического соперничества США и СССР прежде всего в военной сфере, а затем и жесткой глобальной экономической конкуренции по всем направлениям.
Совершенствование формализующих возможностей математического аппарата теоретического представления зубчатых колес и зацеплений стимулировалось использованием в них неэвольвентных профилей для специальных механизмов, целесообразностью проведення соответствующих виртуальных исследований конструкций таких колес и механизмов, технологий их материализации, технической эксплуатации для обоснованных решений с позиций обеспечения ускорения разработок, их промышленного и эксплуатационного освоения, функционального качества и долговечности, Примером такой разработки, потребовавшей инновационной перестройки соответствующих производств механической обработки на предприятиях военно-промышленного комплекса, транспортного машиностроения, т. е. в отраслях промышленности, которые традиционно относятся к определяющим экономический уклад ведущих стран с развитой экономикой, являются двухпараметрические передачи на основе зубчатых колес с постоянным нормальным шагом и эквидистантными линиями зубьев на разных поверхностях вращения. Синтезу вариаторов на основе таких колес посвятил свою работу [2] один из видных конструкторов-танкостроителей XX века В. Р. Ковалюх [3]. В таких передачах есть возможность изменять взаимное положение зубчатых колес и углов скрещивания их осей во время передачи крутящего момента.
Математической базой представленного здесь задания и исследования кинематических схем и определяемых ими способов формообразования конических зубчатых колес с постоянным нормальным шагом и эквидистантными линиями зубьев для вариаторов [2] послужила теория отображения аффинного пространства и ее прикладная разработка научной школой проф. Б. А. Перепелицы и его учеников в Харьковском политехническом институте (НТУ «ХПИ») [4-10].
Обращение к предметно адаптированной теории отображения аффинного пространства [6] позволило создать компактные, структурно унифицированные геометрические модели формообразования и рассмотреть соответствующие им кинематические схемы [10] (таблица № 1).
Таблица № 1
Способы и схемы нарезания конических колес с постоянным нормальным шагом
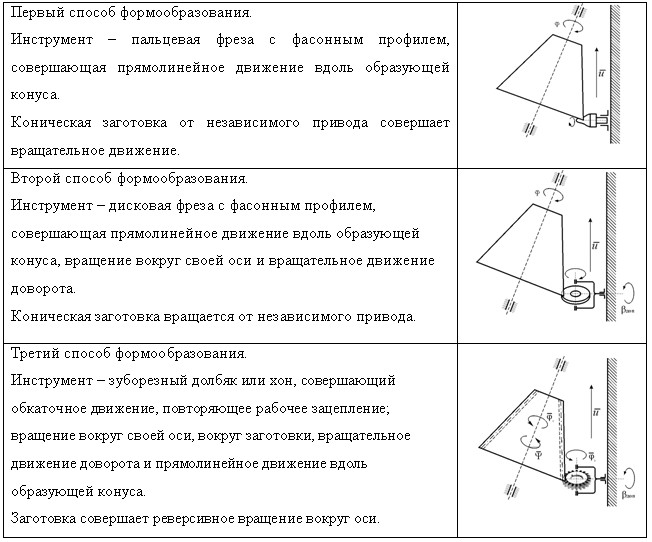
При создании моделей формообразования учитывались конструкторские требования – обеспечение необходимого межцентрового расстояния и диапазона изменения угла скрещивания осей, а также обеспечение показателей качества – постоянства пятна контакта и использования всей поверхности сложного профиля зуба по всей его длине, что обеспечивает повышение несущей способности, уменьшение шумности, массы и габаритов изделия.
В исследуемых передачах зубчатые колёса имеют близкое к точке пятно контакта, это вызывает высокие давление и температуру в этой зоне, следовательно, при создании моделей формообразования этой особенности уделено особое внимание. При моделировании решается обратная задача формообразования, в которой определяется не инструментальная, а формообразуемая поверхность зуба при заданных движениях инструмента относительно заготовки.
Примененный при моделировании и исследованиях математический метод 3D моделирования позволил провести параллель между образованием среза и формообразованием. Формообразуемый элемент представлен пересечением множеств точек, одновременно принадлежащих поверхности резания и заданной поверхности обрабатываемой детали [11].
Исследовались три модели формообразования, основанные на копирующих и обкаточных фасонных инструментах с линейным касанием и обкаточных с точечным касанием. Все модели включают уравнения исходного положения винтовой линии зуба с постоянным нормальным шагом и переменным углом наклона, формообразующего элемента и движения вдоль линии зуба, и описываются в операторной, матричной и параметрической формах записи. Это позволило значительно упростить процесс их сравнительного анализа.
В первой модели формообразующим элементом является режущая кромка фасонного инструмента, совершающая формообразующее движение вдоль линии зуба обрабатываемого колеса. В течение всего цикла формообразования формообразующая линия контактирует с формообразуемой поверхностью зуба всеми своими точками, следовательно, эта поверхность является кинематической и совпадающей с поверхностью резания. Эта модель в матричной форме представлена уравнением (1):
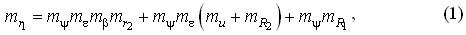
где ![]() – матрицы исходного положения;
– матрицы исходного положения; ![]() – матрицы движений;
– матрицы движений; ![]() – матрицы описания кромки фасонного инструмента.
– матрицы описания кромки фасонного инструмента.
Во второй модели формообразующий элемент основан на инструментальной поверхности вращения с фасонным профилем, имеющей мгновенное линейное касание с формообразуемой поверхностью. В этом случае поверхность впадины находится как однопараметрическая огибающая семейства производящих поверхностей при относительном движении. Необходим также дополнительный доворот формообразующего элемента при передвижении его вдоль линии зуба. Эта модель представлена уравнением (2):
![]()
где введены дополнительные матрицы движения доворота ![]() и относительного движения инструмента
и относительного движения инструмента ![]() .
.
В третьей модели формообразующий элемент представляет собой двухпараметрическое семейство производящих поверхностей с точечным касанием с формообразуемой боковой поверхностью зуба колеса. В этом случае моделируется станочное зацепление, которое совпадает с рабочим (3).
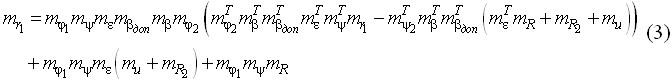
Все рассмотренные модели, как отмечалось выше, включают начальное положение инструмента относительно заготовки, а также подачу вдоль линии зуба с параметрами параллельного переноса и одновременного вращения вокруг оси заготовки. В них имеет место постоянное усложнение кинематики путем наращивания количества движений при переходе от первого ко второму и к третьему способу формообразования. В реализации этих кинематических схем на станках с ЧПУ соответственно достижимы различное качество и себестоимость обработки.
Формообразование по первому способу весьма проблемно по точностным возможностям, особенно в рассмотрении относительно более интенсивного износа фасонного инструмента с потерей заданной формы и, соответственно, более частой его сменой, установкой и наладкой на станке. Эта схема может служить для предварительной обработки.
Вторая модель является более точной, но имеет два существенных ограничения, присутствующих и в первой модели: линейный контакт инструментальной поверхности ограничивает получение точного бокового профиля, а необходимость введения механизма деления приводит к накопленной ошибке на последнем зубе. Данный способ можно использовать в производстве колес со средними показателями качества.
Третий способ исключает все перечисленные выше недостатки, однако требует дорогого оборудования. Этот способ позволяет получать теоретически точные профили боковых поверхностей, а также вести обработку методом обкатки, что позволяет изготавливать исследуемые колеса с высокими показателями качества в рассмотрении в целом.
Современная схематизация обобщенной кинематической схемы формообразования зубчатых звеньев различных классов, типов и видов, исходящая из того же взаимного рассмотрения формообразующего и формообразуемого зубчатых звеньев, аналогично [6] опирается на использование отображений аффинного пространства.
Соответствующий опыт известен в Украине, России, Германии, например, с рассмотрением числа отображений аффинного пространства в качестве признака классификации кинематических схем [12], что позволяет производить разбивку обобщенной кинематической схемы формообразования на подмножества кинематических схем для их реализации при компоновке многокоординатных зубообрабатывающих станков, проектируемых для изготовления зубчатых колес определенного номенклатурного множества.
Литература:
1. Radzevich, S. P. Theory of gearing: Kinematics, Geometry, and Synthesis, Second Edition / S. P. Radzevich. – Boca Raton, Florida: CRC Press, 2018. – 898 p.
2. Ковалюх, В. Р. Синтез зубчатых вариаторов на основе колес с равновысокоширокими зубьями и впадинами : дис. ... канд. техн. наук : 05.02.18. – теория механизмов, машин и автоматических линий / В. Р. Ковалюх. – Харьков, 1982. – 206 с.
3. Танки и люди. Дневник главного конструктора А. А. Морозова / [авт.-сост. В. Л. Чернышев]. – Харьков : [ХИТВ], 2007. – 275 с.
4. Перепелица, Б. А. О геометрических фигурах как аффинных многообразиях / Б. А. Перепелица // Прикл. геометрия и инженер. графика. – Вып. 24. – Киев, 1974. – С. 47-48.
5. Перепелица, Б. А. Режущие инструменты как аффинные многообразия / Б. А. Перепелица // Резание и инструмент. – Вып.16. – Харьков : Изд-во при Харьк. гос. ун-те изд. об-ния «Вища шк.», 1976. – С. 36-40.
6. Перепелица, Б. А. Отображения аффинного пространства в теории формообразования поверхностей резанием / Б. А. Перепелица. – Х. : Вища шк., 1981. – 152 с.
7. Перепелица, Б. А. Автоматизированное профилирование режущих инструментов (теория и алгоритмы) : Учеб. пособие / Б. А. Перепелица. – Харьков : ХПИ, 1985. – 107 с.
8. Разработка теории трехмерного (3D) геометрического моделирования режущих инструментов и процессов формообразования поверхностей на основе многопараметрических отображений аффинного пространства: Отчет о НИР (заключит.) / Нац. техн. ун-т «Харк. политехн. ин-т»; рук. Б. Перепелица. – Харьков, 2001. – 448 с. – № ГР 0100U001083. Инв. № 0202U002517.
9. Перепелица, Б. А. Системы параметров отображений пространства в приложении к 3D-моделированию / Б. А. Перепелица // Сучасні технології у машинобудуванні: Харьков, НТУ „ХПІ”, 2006. – Т. 1. – С. 402-408.
10. Создание теории унифицированной многопараметрической информационной базы для CAD/CAM систем зубчатых зацеплений, инструментов и процессов зубообработки : Отчет о НИР (заключит.) / Нац. техн. ун-т «Харк. политехн. ин-т»; рук. Б. Перепелица и В. Доброскок. – Харьков, 2009. – 452 с. – № ГР 0108U001445. – Инв. № 0210U001273.
11. Перепелица, Б. А. Автоматизированное профилирование режущих инструментов (теория и алгоритмы) : Учеб. пособие / Б. А. Перепелица. – Харьков : ХПИ, 1985. – 107 с.
12. Кривошея, А. В. К вопросу классификации кинематических схем и математических моделей формообразования зубчатых передач / А. В. Кривошея, Ю. М. Данильченко, М. Г. Сторчак, Д. Т. Бабичев и др. // Вісн. Нац. техн. ун-ту «ХПІ». – 2014. – № 31. – С. 75-84.

