Гончар Ігор Володимирович, студент
НТУУ «КПІ ім. Ігоря Сікорського»
місто Київ, Україна
Синиця Валентин Іванович, доцент
НТУУ «КПІ Ім. Ігоря Сікорського»
місто Київ, Україна
Анотація: В наш час, комп’ютерні технологій широко використовуються в учбовому процесі. Одна з областей використання цієї технології є впровадження в учбовий процес програмно-методичних комплексів. Представлений в даній статті програмно-методичний комплекс призначений для дослідження амплітудної та частотної модуляції. Представлено програмній код в середовищі MATLAB для дослідження модульованих сигналів .
Ключові слова: амплітудна модуляція, частотної модуляція, коефіцієнт амплітудної модуляції, девіація частоти, індекс частотної модуляції.
1. Амплітудна модуляція
Модуляція-це процес зміни в часі за заданим законом параметрів якогось з фізичних процесів. В радіотехніці таким фізичним процесом є гармонійне коливання, яке називають частотою носієм (опорною частотою) :
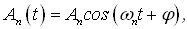
де 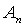 - амплітуда сигналу-носія,
- амплітуда сигналу-носія, 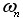 - частота сигналу-носія,
- частота сигналу-носія, 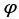 - початкова фаза,
- початкова фаза, 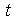 - час.
- час.
Амплітудна модуляція(АМ)— вид модуляції, при якій параметром сигналу-носія, що змінюється, є амплітуда його коливань.[1]
Для більш детального аналізу характеристик амплітудно-модульованих сигналів розглянемо сигнал, в якому в модулюючого сигналу виступає гармонічне коливання.
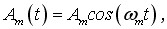
де 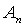 - амплітуда сигналу,
- амплітуда сигналу, 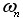 - частота сигналу,
- частота сигналу, 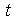 - час.
- час.
Форма запису амплітудно-модульованого сигналу:
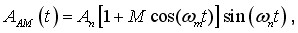
де 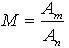 -коефіцієнт амплітудної модуляції (глибина модуляції).
-коефіцієнт амплітудної модуляції (глибина модуляції).
На рисунку 1 представлені отримані в результаті комп'ютерного моделювання часові реалізації АМ сигналів і їх спектри. Розрахунок характеристик даної моделі був зроблений при наступних параметрах: амплітуда сигналу-носія Аn = 4 V; частота fn = 20 kHz ; амплітуда модулюючого сигналу Аm = 2 V; частота fm = 2 kHz; коефіцієнт амплітудної модуляції М = 0.5; 1; 1.5.
З ростом коефіцієнту амплітудної модуляції М ростуть амплітуди бічних складових сигналу 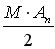 , віддалені від частоти-носія на частоту модулюючого сигналу. При М>1 виникає перемодуляція, при якій форма обвідної спотворюється щодо форми модулюючого сигналу.
, віддалені від частоти-носія на частоту модулюючого сигналу. При М>1 виникає перемодуляція, при якій форма обвідної спотворюється щодо форми модулюючого сигналу.
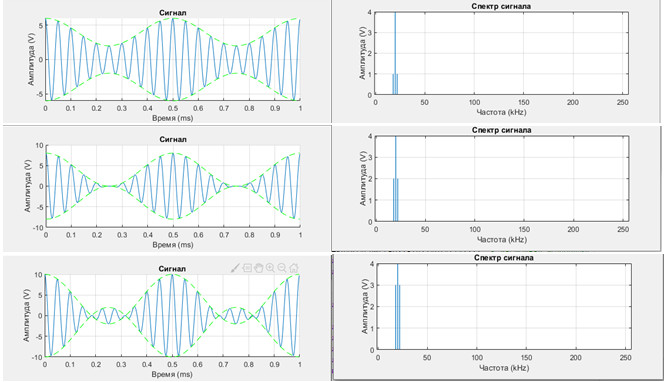
Рис. 1. Часові реалізації АМ-сигналів (зліва) і їх спектри (праворуч) при різних значеннях коефіцієнту амплітудної модуляції (М = 0,5; 1; 1,5) .
2. Частотна модуляція
Частотна модуляція (ЧМ)— вид модуляції, за якого частота вихідного сигналу змінюється у часі залежно від миттєвого значення інформаційного сигналу, тобто інформаційний сигнал керує частотою опорного сигналу. У порівнянні з амплітудною модуляцією, ідеальна частотна модуляція не вносить змін в амплітуду несучої. [1]
Форма запису частотно-модульованого сигналу:
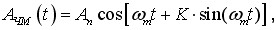
де 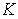 - індекс частотної модуляції.
- індекс частотної модуляції.
Індекс частотної модуляції визначається як 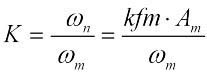 - відношення максимальної девіації частоти (за один період модулюючого сигналу) до частоти модуляції.
- відношення максимальної девіації частоти (за один період модулюючого сигналу) до частоти модуляції.
 -розмірний коефіцієнт пропорційності.
-розмірний коефіцієнт пропорційності.
Амплітуда спектральних складових ЧМ коливання визначається величиною індексу частотної модуляції. При вузько смуговій ЧМ (K<<1) амплітудний спектр ЧМ коливання збігається зі спектром АМ коливання. При великих індексах модуляції (K>>1) ширина спектра ЧМ коливання близька до подвоєної девіації частоти.
На рисунку 2 представлені отримані в результаті комп'ютерного моделювання часові реалізації ЧМ сигналів і їх спектри. Розрахунок характеристик даної моделі був зроблений при наступних параметрах: амплітуда сигналу-носія Аn = 2 V; частота fn = 20 kHz ; амплітуда модулюючого сигналу Аm = 2 V; частота fm = 2 kHz; індекс модуляції М = 1; 4; 8.
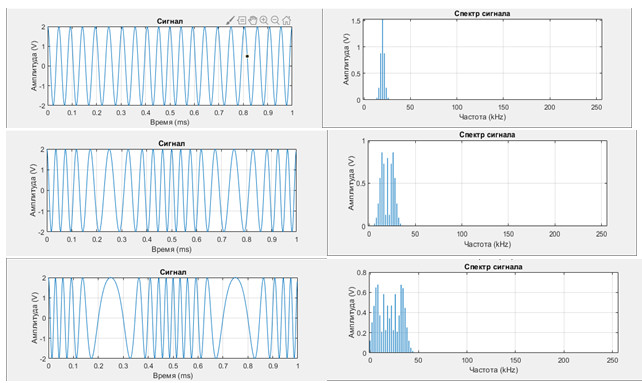
Рис. 2. Часові реалізації ЧМ-сигналів (зліва) і їх спектри (праворуч) при різних значеннях індексів частотної модуляції (М = 1; 4; 8) .
3. Програмній код в середовищі MATLAB
clc; % Очистка
clear all % Очистка памяти
%% Параметры
Am = input('Введите амплитуду сигнала (V): ');
fm = input('Введите частоту сигнала (kHz): ');
Fd = input('Введите частота дискретизации : ');
FftL=Fd; % Количество линий Фурье спектра
dt = 1/Fd; % шаг
Tm = input('Введите время моделированния (ms) : ');
t = (0:dt:Tm-dt)'; % масив отсчета времени
An = input('Введите амплитуду несущего сигнала (V): ');
Fn = input('Введите частоту несущего сигнала (kHz): ');
Kam = input('Введите коэффициент модуляции : ');
Kfm = input('Введите коэффициент пропорциональности частотной модуляции : ');
var= input('Форма исходного сигнала: 1-Синусоидальный; 2-Меандр');
switch var
case 1
Signal = Am*cos(2*pi*fm*t); % сигнал
Signaln = An*cos(2*pi*fn*t); % несущий сигнал
Sam=An*(1+(Kam*Am/An)*cos(2*pi*fm*t)).*cos(2*pi*fn*t); % амплитудная модуляция
Sfm=An*cos(2*pi*fn*t+(Kfm*Am/(2*pi*fm))*sin(2*pi*fm*t)); % частотная модуляция
case 2
Signal =Am*square(2*pi*fm*t); % сигнал
Signaln = An*cos(2*pi*fn*t); % несущий сигнал
Sam=(An+Kam*Signal).*cos(2*pi*fn*t); % амплитудная модуляция
Sfm=An*cos(2*pi*fn*t+Kfm*Am*cumtrapz(square(2*pi*fm*t))); % частотная модуляция;
end;
%% Спектральное представление сигнала
FftS=abs(fft(Signal,FftL)); % Амплитуды преобразования Фурье сигнала
FftS=2*FftS./FftL; % Нормировка спектра по амплитуде
FftS(1)=FftS(1)/2; % Нормировка постоянной составляющей в спектре
Fftn=abs(fft(Signaln,FftL)); % Амплитуды преобразования Фурье сигнала
Fftn=2*Fftn./FftL; % Нормировка спектра по амплитуде
Fftn(1)=Fftn(1)/2; % Нормировка постоянной составляющей в спектре
FftA=abs(fft(Sam,FftL)); % Амплитуды преобразования Фурье сигнала
FftA=2*FftA./FftL; % Нормировка спектра по амплитуде
FftA(1)=FftA(1)/2; % Нормировка постоянной составляющей в спектре
Ffth=abs(fft(Sfm,FftL)); % Амплитуды преобразования Фурье сигнала
Ffth=2*Ffth./FftL; % Нормировка спектра по амплитуде
Ffth(1)=Ffth(1)/2; % Нормировка постоянной составляющей в спектре
F=0:Fd/FftL:Fd/2-1/FftL; % Массив частот вычисляемого спектра Фурье
%% Построение графиков
figure('Name','Сигнал и Спектр');% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
plot(t,Signal);% Построение сигнала
grid;
title('Сигнал');% Подпись графика
xlabel('Время (ms)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
bar(F,FftS(1:length(F)));% Построение спектра Фурье сигнала
grid;
title('Спектр сигнала');% Подпись графика
xlabel('Частота (kHz)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
figure('Name','Несущий сигнал и Спектр');% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
plot(t,Signaln);% Построение сигнала
grid;
title('Сигнал');% Подпись графика
xlabel('Время (ms)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
bar(F,Fftn(1:length(F)));% Построение спектра Фурье сигнала
grid;
title('Спектр сигнала');% Подпись графика
xlabel('Частота (kHz)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
figure('Name','Амплитудная модуляция');% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
hold on
plot(t,Sam);% Построение сигнала
plot(t, An*(1+(Kam*Am/An)*cos(2*pi*fm*t)), '--', 'Color', 'green'); % график огибающей
plot(t, -1*An*(1+(Kam*Am/An)*cos(2*pi*fm*t)), '--', 'Color', 'green'); % график огибающей
grid;
hold on
title('Сигнал');% Подпись графика
xlabel('Время (ms)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
bar(F,FftA(1:length(F)));% Построение спектра Фурье сигнала
grid;
title('Спектр сигнала');% Подпись графика
xlabel('Частота (kHz)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
figure('Name','Частотная модуляция');% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
plot(t,Sfm);% Построение сигнала
grid;
title('Сигнал');% Подпись графика
xlabel('Время (ms)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
bar(F,Ffth(1:length(F)));% Построение спектра Фурье сигнала
grid;
title('Спектр сигнала');% Подпись графика
xlabel('Частота (kHz)');% Подпись оси х графика
ylabel('Амплитуда (V)');% Подпись оси у графика
Висновок
Застосування програмно методичного комплексу для дослідження модульованих сигналів в навчальному процесі значно спростить процес вивчення та дослідження модуляції сигналів, скорочує час на навчання, дозволяє більш адекватно оцінити рівень отриманих знань та навичок, при необхідності дозволити виконати роботу дистанційно.
Література:
1. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник. – М.: Высшая школа., 1983. - 536 с.
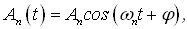
![]() - амплітуда сигналу-носія,
- амплітуда сигналу-носія, 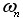 - частота сигналу-носія,
- частота сигналу-носія, ![]() - початкова фаза,
- початкова фаза, 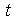 - час.
- час.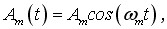
![]() - амплітуда сигналу,
- амплітуда сигналу, 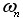 - частота сигналу,
- частота сигналу, 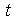 - час.
- час.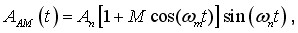
![]() -коефіцієнт амплітудної модуляції (глибина модуляції).
-коефіцієнт амплітудної модуляції (глибина модуляції).![]() , віддалені від частоти-носія на частоту модулюючого сигналу. При М>1 виникає перемодуляція, при якій форма обвідної спотворюється щодо форми модулюючого сигналу.
, віддалені від частоти-носія на частоту модулюючого сигналу. При М>1 виникає перемодуляція, при якій форма обвідної спотворюється щодо форми модулюючого сигналу.
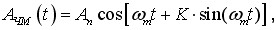
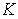 - індекс частотної модуляції.
- індекс частотної модуляції.![]() - відношення максимальної девіації частоти (за один період модулюючого сигналу) до частоти модуляції.
- відношення максимальної девіації частоти (за один період модулюючого сигналу) до частоти модуляції. 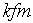 -розмірний коефіцієнт пропорційності.
-розмірний коефіцієнт пропорційності.

