Сингх Денис Лахвиндерович
студент
НТУУ «Киевский политехнический институт им. Игоря Сикорского»
город Киев, Украина
Шведова Виктория Викторовна
доцент
НТУУ «Киевский политехнический институт им. Игоря Сикорского»
город Киев, Украина
Аннотация: Предложено методическое обеспечение тренажера для оценивания динамической погрешности мехатронного аэромаятника, которое предполагает исследование его динамических параметров.
Ключевые слова: динамические характеристики, динамическая погрешность, диференциальное уравнение, передаточная функция, аэромаятник, учебный тренажер.
В настоящий момент использование тренажеров в учебном процессе позволяет повысить эффективность учебного процесса, за счет предварительной отработки навыков работы с системами управления.
Их эффективное применение в учебном процессе значительно уменьшает число ошибок, сокращает время на обучение, позволяет более адекватно оценить уровень полученных знаний и полученных навыков, увеличивает скорость манипуляций и индивидуализирует обучение [1]. Востребованность в тренажерах появилась из-за достаточно высокой стоимости оборудования, их недостаточным количеством, затратами на использование и сложности в эксплуатации реального оборудования.
Основой для построения тренажера для измерения динамических характеристик мехатронного аэромаятника есть макет, созданный Университетом Аризоны и описан в статье Mechatronic Aeropendulum: Demonstration of Linear and Nonlinear Feedback Control Principles With MATLAB/Simulink Real-Time Windows Target [2].
1. Исследование уравнения передаточной функции аэромаятника в динамическом режиме
Нелинейная динамическая модель маятника представляется выражением:
где 
- угол поворота стержня, 
- первая производная от угла поворота стержня, 
- вторая производная от угла поворота стержня,
- вес двигателя, 
- длина маятника, 
- коэффициент трения, 
- сила тяжести маятника.
Используя теоретические сведения и предположение о том, что при малых углах отклонения 
необходимо вывести выражение для передаточной функции аэромаятника, описываемого моделью, что и предлагается сделать студентам
Примечание: должно получиться выражение для передаточной функции вида:
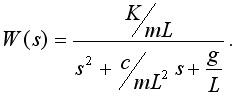
2. Исследование параметров переходной характеристики аэромаятника в динамическом режиме на основе эксперимента
Затем необходимо запустить аеромаяник и исследовать его экспериментально полученную переходную функция, которая имеет вид как на рисунке 1:
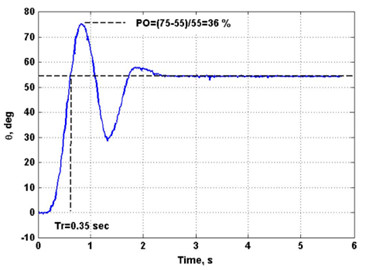
Рис. 1 Експериментальная переходная функція аеромаяка.
По экспериментальной кривой необходимо выразить собственную частоту колебаний маятника 
и коеффициент демпфирования 
.
Примечание: должны получиться выражение вида:
Для нахождения частоты собственных колебаний нужно установить задаваемый угол на уровне 90 градусов и зафиксировать изменение результирующего угла с помощью макета и программы AeropendulumSOFT.mdl.
Необходимо оценить период собственных колебаний системы 
.
Исходя их этого находят значение собственной частоты колебания системы и время установления как:
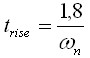
Затем необходимо вывести выражения для импульсной и переходной характеристик
Примечание: при упрощении модели, принимая 
должны получиться выражение вида
- Импульсная характеристика
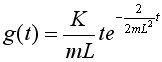; - Переходная характеристика
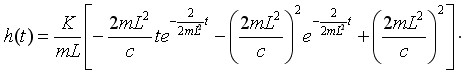
3. Нахождение динаминаческой погрешности системы
Задачей является нахождение относительной и абсолютной динамической погрешности системы, на основе найденных ранее характеристик (параметров) аеромаяника.
Относительная динамическая погрешность не зависит от свойств входного сигнала и зависит лишь от свойств динамической системы.
Относительную динамическую погрешность определяют по формуле:
где 
- статический коэффициент преобразования.
Студентам необходимо найти относительную погрешность в операторной форме.
Примечание: должны получиться выражение вида:
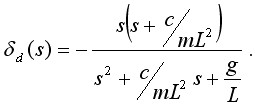
Абсолютная динамическая погрешность зависит и от свойств динамической системы и от вида входного сигнала.
Далее находят абсолютную погрешность в операторной форме.
Примечание: должно получиться выражение вида:
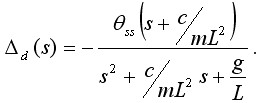
Абсолютную погрешность во временной области получают с использование преобразования Лапласа от выражения, представленного в операторной форме.
Нужно найти абсолютную погрешность во временной области и схематически постройте его график.
Примечание: должны получиться выражение вида:
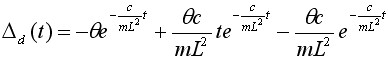
Литература
1. Интерактивные тренажеры и их значение в учебном процессе https://novainfo.ru/article/4403
2. Advanced Micro and Nano Systems Laboratory, Department of Aerospace and Mechanical Engineeringo University of Arizona https://www.researchgate.net/publication/260587270
