Шведова Вікторія Вікторівна

кандидат технічних наук, 

доцент кафедри інформаційно-вимірювальної техніки

Національного технічного університету України 

«Київський політехнічний інститут ім. І.Сікорського»

Україна, Київ

 

Півторак Анастасія Ігорівна

студент

 Національного технічного університету України 

«Київський політехнічний інститут ім. І.Сікорського»

Україна, Київ

 

 Анотація: Запропоновано спосіб ідентифікації параметрів динамічних об’єктів не вище другого порядку за експериментальними даними. 

 Ключові слова: динамічна ланка, коливальний режим, аперіодичний режим, критичний режим.

 

 Проведений аналіз динамічних ланок, що проявляють свою роботу в трьох режимах в залежності від значення коефіцієнту демпфірування β [1]:

• якщо β=1, то динамічна система працює у критичному режимі;
• якщо β>1, система в аперіодичному режимі;
• якщо β<1, система знаходиться в коливальному режимі.

 На малюнку 1 показано, як виглядає крива відгуку системи на ступінчатий сигнал у випадку: 1 - періодичний режим, 2 - аперіодичний режим та 3 - критичний режим.

 

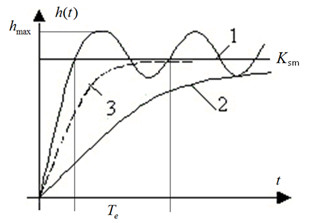
 Мал.1 Варіанти відгуку системи на ступінчатий сигнал

 У випадку аперіодичного режиму роботи системи (β>1) її перехідна характеристика (малюнок 2) схожа на перехідну характеристику ланки першого порядку, що ускладнює знаходження параметрів системи за експериментальними даними.

 

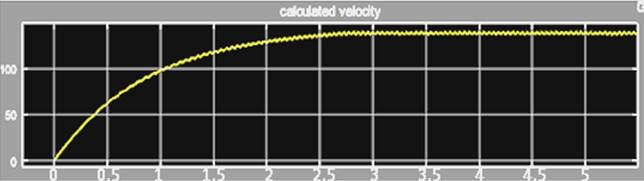
Мал.2. Перехідна характеристика аперіодичного об’єкту другого порядку

 Передаточна функція системи має вигляд:

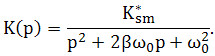
 Передаточна функція в статичному режимі має вигляд:

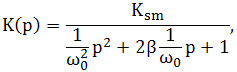
 де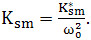 

 Або можна представити у вигляді:

 де x₁,x₂ – полюса рівняння.

 Корні рівняння знаходять:

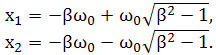
 Якщо β=1, полюса рівняння  x₁=x₂=-βω₀, тобто динамічна система працює у критичному режимі.

 Якщо β>1, полюса дійсні, тобто система в аперіодичному режимі. 

 Якщо β<1, маємо комплексні корні рівняння:

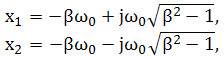
 тобто система знаходиться в коливальному режимі.

 Для вирішення задачі знаходження параметрів системи можна використовувати метод передачі елементів з двома різними константами часу. Для цього знаходять першу похідну перехідної характеристики:

 

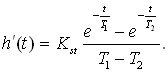
 Для знаходження перегину функції прирівнюють другу похідну до нуля:

 

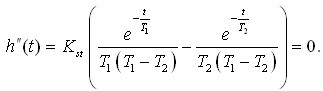
 Розраховується час повороту:

 

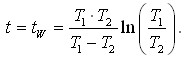
 Максимальне значення функції знаходять за формулою:

 

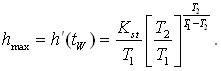
 Розрахунок рівноважного часу:

 

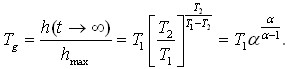
 Розрахунок затримки:

 

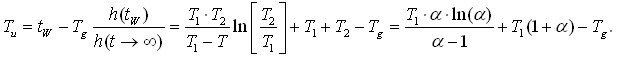
 З цих рівнянь знаходять необхідні параметри динамічної об’єкту. 

 Але згідно з методом на експериментальному графіку повинно чітко бути видно перегин функції, що не завжди відповідає практичній реалізації. Виходячи з цього для аперіодичної ланки другого порядку пропонується альтернативний підхід для знаходження параметрів системи. 

 Для теоретичного рівняння:

 

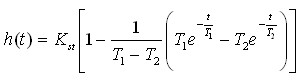
 за відомими точками складають експериментальне  рівняння. За допомогою комп’ютерної техніки можна знайти параметри експериментального рівняння, що дозволяє визначити параметри системи.

 Результат експерименту дозволяє знайти параметри системи другого порядку (K_sm,T₁, T₂,), виконавши вимірювання в трьох точках на рівні 20%, 80% та близько 100% від K_sm. Ці точки однозначно визначають поведінку системи.

 

Література:

1. Попович М.Г. Теорія автоматичного керування: Підручник /М.Г. Попович, О.В. Ковальчук. – К.: Либідь, 1997. – 517с.