Морозова Мария Николаевна,

кандидат технических наук, 

НТУУ «КПИ им. Игоря Сикорского»,

Украина, г. Киев

 Аннотация: Принцип действия индуктивных датчиков состоит в преобразовании величины измеряемого размера в полное сопротивление катушки индуктивности. Датчик представляет собой катушку индуктивности или взаимной индуктивности того или иного вида. 

Наиболее часто в качестве датчиков размера используются катушки индуктивности с ферромагнитными сердечниками. Индуктивность такой катушки при малых величинах немагнитных зазоров в магнитопроводе описывается формулой: 

 ,

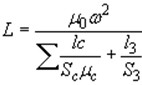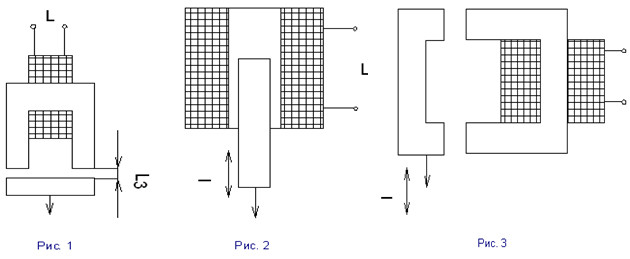
 где µ₀ - магнитная постоянная; ω - число витков катушки; l_c , S_c , µ_c - длина, площадь сечения и относительная магнитная проницаемость участков ферромагнитного сердечника соответственно; l₃ , S₃  - длина и площадь немагнитных зазоров в сердечнике. Из этой формулы следует, что при изменении длины l₃  или площади S₃ немагнитных зазоров в сердечнике изменяется индуктивность катушки. Этот принцип используется в индуктивных датчиках с переменным зазором и переменной площадью. Пусть с изменением измеряемого размера связано изменение длины немагнитного зазора  l₃ (рис. 1). В этом случае произойдет относительное изменение индуктивности L : 

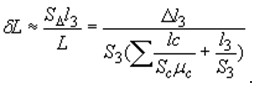
 Поскольку для катушки с сердечником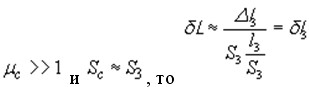   

 С помощью электрических методов можно измерить  , что эквивалентно относительному изменению  . На рис. 1 и рис. 3 приведены схемы контактного датчика размера с катушкой индуктивности, имеющей ферромагнитный сердечник. Сердечник катушки разделен на две части - неподвижную, называемую собственно сердечником и несущую катушку индуктивности, и подвижную, закрепленную на измерительном стержне и называемую якорем. Изменение размеров детали или ее перемещение приводит к перемещению якоря относительно сердечника и к изменению немагнитного зазора в магнитопроводе катушки. Последнее вызывает изменение индуктивности катушки и, следовательно, изменение полного сопротивления: 

 где R_n - активное сопротивление потерь катушки, ω - круговая частота питающего катушку тока. Модуль полного сопротивления катушки датчика по переменному току: 

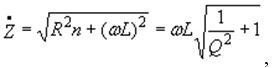
 где  - добротность индуктивного датчики. Можно построить и бесконтактный индуктивный датчик, используя схему, приведенную на рис. 1. В этом случае якорем служит сама контролируемая деталь, и через нее замыкается магнитный поток, создаваемый катушкой в сердечнике. Изменение размера детали ведет к изменению зазора l₃  и к изменению индуктивности катушки L . По бесконтактной схеме можно контролировать как ферромагнитные, так и неферромагнитные металлические детали. В последнем случае датчик работает с использованием эффекта вихревых токов. Индуктивный датчик может быть построен по схеме с перемещением в магнитном поле катушки ферромагнитного разомкнутого сердечника (рис. 2). Такие датчики называют соленоидальными.

 По схеме построения датчики можно разделить на одинарные и дифференциальные (рис.4а,б). Одинарный датчик содержит одну измерительную ветвь, дифференциальный - две. В дифференциальном датчике при изменении измеряемого параметра одновременно изменяются индуктивности двух одинаковых катушек, причем изменение происходит на одну и ту же величину, но с обратным знаком (зеркально). При воздействии входной величины Δl  полное сопротивление преобразователя получает приращение ΔZ . Однако величина  Z зависит не только от входной величины l , но и от ряда других факторов, приводящих к изменению l  и Q . Пусть суммарная относительная нестабильность полного сопротивления преобразователя под действием помех равно ϒ_c . В этом случае относительная погрешность преобразователя в диапазоне изменения входной величины D=Δl  равна: 

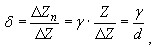
 где ϒ - относительная нестабильность полного сопротивления преобразователя под действием помех; Z - полное сопротивление преобразователя; ΔZ - приращение полного сопротивления, соответствующее диапазону измерения Δl ; d - относительное изменение полного сопротивления в диапазоне измерения D . Так как всегда ΔZ<Z и d<l , то δ<γ . Следовательно, для одинарного индуктивного преобразователя относительная погрешность в рабочем диапазоне всегда больше относительной нестабильности его полного сопротивления под действием помех. Дифференциальный индуктивный преобразователь состоит из двух простых одинаковых преобразователей. Под действием входной величины Δl  полное сопротивление обоих преобразователей Z₁ и Z₂  изменяется зеркально, т.е. на одну и ту же величину, но с разным знаком. Схема включения дифференциального преобразователя реагирует на алгебраическую разность Z₁ - Z₂ , за счет чего его чувствительность повышается в 2 раза по сравнению с одинарным. При идеальной симметрии дифференциального преобразователя его относительная погрешность в диапазоне  D : 

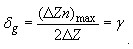
 Реально дифференциальный преобразователь всегда обладает асимметрией, которая может выражаться в том, что: а) в нулевой точке Z₁ ≠ Z₂ ; б) чувствительность к входному перемещению у обеих половин преобразователя неодинакова; в) коэффициенты нестабильности у обеих половин преобразователя также неодинаковы. При рассмотрении зависимости погрешности дифференциального преобразователя от наличия асимметрии можно увидеть, что асимметрия вида а) и в) приводит к возрастанию погрешности преобразователя. Одновременное присутствие всех видов асимметрии приведет к тому, что относительная погрешность дифференциального преобразователя в диапазоне измерения D  будет равна: 

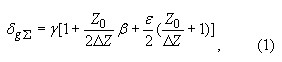
 где Z₀ - полное сопротивление каждой половины преобразователя при нулевом положении подвижного якоря; ΔZ - полное изменение полного сопротивления одной половины преобразователя, соответствующее диапазону измерения D ;  - коэффициент асимметрии половин преобразователя при нулевом положении подвижного якоря (при этом предполагается   - коэффициент асимметрии показателей нестабильности половин преобразователя. Предполагается  . Из выражения (1) следует, что при наличии асимметрии у дифференциального преобразователя его погрешность увеличивается. В реальных конструкциях преобразователей асимметрия всегда имеет место и ориентировочно составляет   в зависимости от тщательности исполнения и настройки преобразователя. Сравним одинарный и дифференциальный преобразователи при наличии у последнего асимметрии 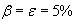 . Пусть  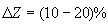. Тогда 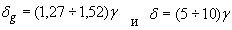. Соотношение погрешностей  , т.е. выигрыш в точности у дифференциального преобразователя составляет   раз. Этот выигрыш тем меньше, чем больше асимметрия. 

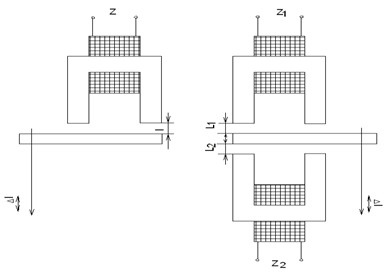
Рис. 4 

Литература

1. Теория и расчет индуктивных датчиков перемещений для систем автоматического контроля: монография / А.В. Федотов. – Омск: Изд-во ОмГТУ, 2011.