Золовкін Сергій Михайлович
НТУУ «КПІ ім. Ігоря Сікорського»
м. Київ
Для аналізу часових рядів (систем) в умовах повної невизначеності (не є нормально-розподіленими або близькими до неї), використовується метод нормованого розмаху (RS-аналіз), запропонований Херстом, який дозволяє розрізнити випадковий і фрактальний тимчасові ряди, а також робити висновки про наявності неперіодичних циклів, довготривалої пам'яті і т.д.
Довгостроковими ефектами або довгою пам'яттю називають кореляційний структуру часових рядів, що мають великі зрушення. R / S -аналіз може показати деяку стійкість (або нестійкість) тренда випадкового процесу, причому стійкість характеризується наявністю довгострокових ефектів.
В основі R / S-аналізу лежить наступне співвідношення:
(R/S)n = СnH,
де n - розмір вибірки;
Н - показник, що визначає довгу або коротку пам'ять (експонента Херста);
R - розмах вибірки;
S - емпірична дисперсія;
С - деяка константа.
Алгоритм розрахунку показника Херста Н заснований на обчисленні нормованого розмаху (RS-аналіз). Для визначення значення H використовується алгоритм R / S-аналізу Тимчасових рядів.
Показник Херста H в поточному часовому вікні оцінюється як нахил кривої прямої лінійної регресії між значеннями ln(R/S(n) і ln(n). Так як значення матимуть деяке відхилення від лінії, нам необхідно знати похибку апроксимування та значимість лінії регресії.
0 <H <1 - постійна, значення якої для більшості метеорологічни спостережень лежить в околі 0.7.
Таким чином математична модель матиме такий вигляд:
1. Розрахуємо логарифмічні відношення для вихідного часового ряду St:
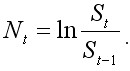
2. Розділимо ряд N на A суміжних періодів довжиною n. Відзначимо кожен період як Ia, де a = 1,2,3 ... A. Визначимо для кожного Ia середнє значення:
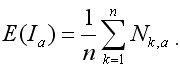
3. Розрахуємо відхилення від середнього значення для кожного періоду Ia:
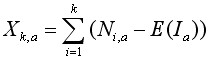
4. Розрахуємо розмах в межах кожного періоду:
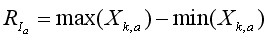
5. Розрахуємо стандартне відхилення для кожного періоду Ia:
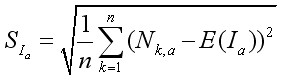
6. Кожен RIa ділимо на SIa. Далі розраховуємо середнє значення R / S:
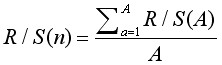
7. Збільшуємо n і повторюємо кроки 2-6 до тих пір, поки n≤N / 2.
9. Будуємо графік залежності 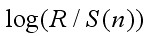 від
від 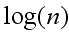 .
.
10.За допомогою метода найменших квадратів знаходимо регресію виду:
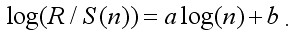
На основі математичної моделі показника Херста була розроблена структурна схема програми розрахунку показника Херста у вигляді алгоритму.
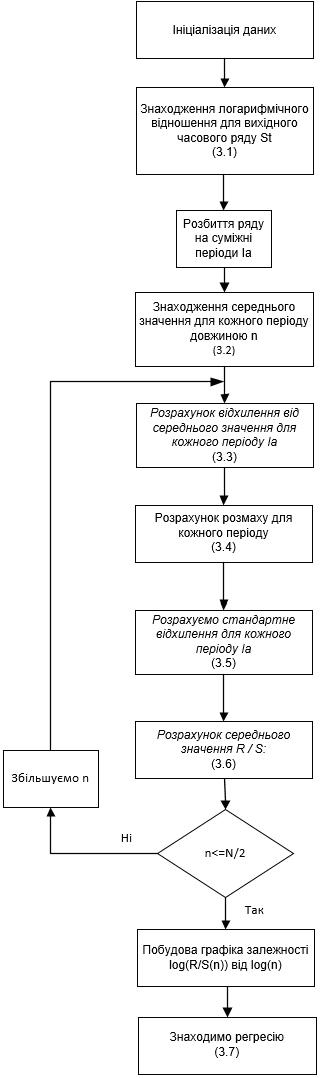
Рисунок.1 – Структурна схема розрахунку показника Херста
На основі структурної схеми програми розрахунку показника Херста, була розроблена блок-схема програми та її реалізація в програмному середовищі MatLab.
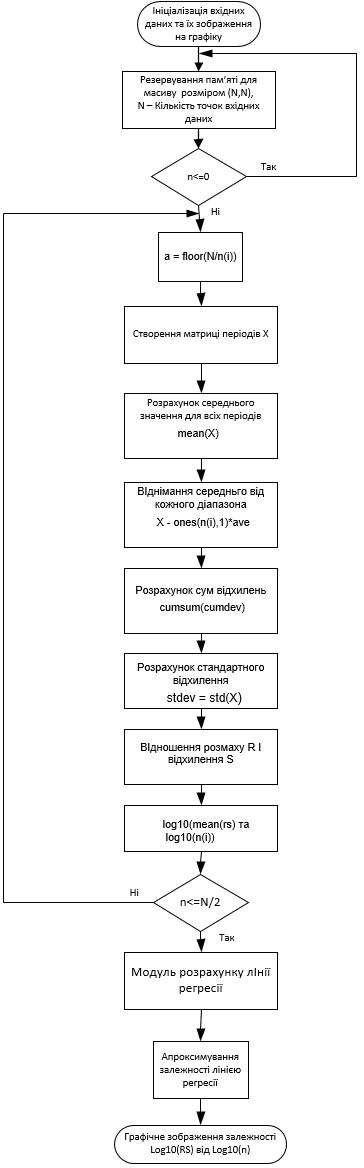
Рисунок. 2 – Блок-схема програми розрахунку показника Херста
Розрахунок показника Херста є основою в багатьох системах моніторингу та прогнозування деформаційних процесів. Написавши програмне забезпечення, можно визначити випадковість чи не випадковість деформаційних процесів на об’єкті моніторингу чи спрогнозувати його. Це дає змогу попередити можливі руйнування об’єкту та запобігти екологічного лиха та матеріального збитку.
Література:
1. Anis, A.A., Lloyd, E.H. (1976) The expected value of the adjusted rescaled Hurst range of independent normal summands. Peters, E.E. (1994) Fractal Market Analysis. Wiley, New York. ISBN 0-471-58524-6.
2. Акустико-эмиссионная диагностика конструкций / А. Н. Серьезнов, Л.Н.Степанова, В. Муравьев, - Радио и свзяь, 2000. - 280 страниц.

