Становський О. Л.

доктор технічних наук, професор

Одеський національний політехнічний університет, Одеса, Україна

Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її.

 

Торопенко А. В.

кандидат технічних наук

Одеський національний політехнічний університет, Одеса, Україна

Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її.

 

Швець П.С.

кандидат технічних наук

Одеський національний політехнічний університет, Одеса, Україна 

Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її. 

 

Торопенко О. В.

Одеський національний політехнічний університет, Одеса, Україна 

Ця електронна адреса захищена від спам-ботів. вам потрібно увімкнути JavaScript, щоб побачити її.

 

 Показано, що зв'язність підсистем при управлінні будівництвом різнотипних комплексів із зв’язаними параметрами створює серйозні проблеми при оптимізації проектних рішень, спрямованих на зниження термінів і вартості будівельних робіт. Розглянуто відмінності в підходах до оптимізації споруд, що містять різні по зв'язності підсистеми, на прикладах інфраструктури будівництва. Наведені моделі зв'язності об'єктів оптимізації і запропонований метод комплексного генетичного алгоритму для її здійснення. 

 Ключові слова: комплекси із зв’язаними параметрами, штучна інфраструктура, зв'язність підсистем, оптимізація рішень, генетичний алгоритм.

 

Зона забудови або будівельний майданчик має в будівництві різнотипних комплексів із зв’язаними параметрами дуже важливе значення, тому що вона вимагає уваги вже на ранній стадії проектування [1]. Навіть якщо мова йде про використання типових проектів споруджень, необхідно постійно піклуватися про їхню прив'язку до реального середовища, що оточує будівництво – його інфраструктуру. 

Виділимо дві підсистеми в інфраструктурі: природну, зовнішню, обумовлену, наприклад, рельєфом місцевості або кліматичною зоною, у якій розташований будмайданчик (мал. 1) [2], і штучну, внутрішню, що складається з комунікаційних інтерфейсів навколо будинків або навіть під ними (наприклад, точок підведення / відводу води, електрики, опалення, каналізації, інформаційних каналів і т.д.) (мал. 2).

  

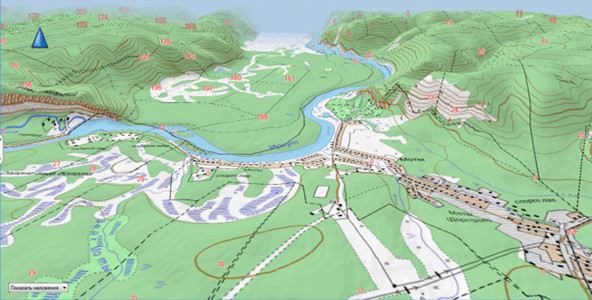
Мал. 1. Зовнішня (природна) підсистема інфраструктури будівництва

 

 

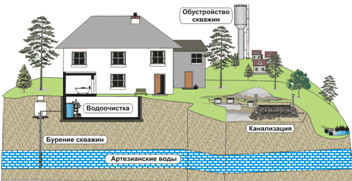
Мал. 2. Внутрішня (штучна) підсистема інфраструктури будівництва

 

 При керуванні проектами та програмами створення комплексу різнорідних споруджень ставиться завдання забезпечення оптимального з погляду вартості та строків будівництва [3]. Рішення завдань оптимізації для об'єктів такого класу, на перший погляд, спрощується тим, що вони, як правило, природно розбиваються на підсистеми (наприклад, основні та допоміжні будинки, підсобні приміщення і т.д.). Однак обчислювальні складності, що виникають при такій розбивці через зв’язність параметрів цих підсистем, на жаль, зводять нанівець всі переваги такого підходу: зростають строки керування та знижується якість об'єкта. Тому створення нових моделей зв’язності та методів оптимізації, що дозволяють вирішити цю проблему, є досить актуальним.

 Авторська розробка присвячена рішенню важливого наукового та практичного завдання зниження строків і підвищення ефективності керування програмами будівництва споруджень за рахунок більш глибокої оптимізації слабозв’язаних систем шляхом розробки та впровадження нових математичних моделей комплексних будівельних об'єктів зі слабозв’язаними елементами та методів їхньої еволюційної оптимізації.

 Під системою розуміють сукупність взаємозалежних елементів, відособлену від середовища та взаємодіючу з нею як ціле [4]. Істотний вплив на поводження елементів системи та властивості її як цілого робить структурна, параметрична, інформаційна і т.д. міра їхніх зв'язків. Це дозволяє говорити про величину цієї міри та виділити, наприклад, класи незв'язаних, слабозв’язаних і сильнозв’язаних систем [5, 6].

 Під слабозв’язаною розуміють таку систему, у якій взаємодія елементів досить сильно для формування системних властивостей, але недостатньо для зміни якісних властивостей окремих елементів [7]. Для систем, утворених елементами зі складною внутрішньою структурою, поняття слабозв’язаної системи не є однозначним. Взаємодія елементів системи може викликати зміну одних характеристик елементів і не впливати на інші. Питання про ідеальність або неідеальність системи в цьому випадку вирішують, виходячи з того, чи є характеристики, що змінюються при взаємодії, істотними для аналізу конкретної системи та конкретної властивості [8].

 Очевидно, що при керуванні проектами та програмами, наприклад, будівництва комплексу будинків і споруджень деякі їхні параметри можуть варіюватися незалежно один від одного (параметри покрівлі), деякі – умовно незалежно, у межах взаємних обмежень (параметри комунікацій і внутрішніх проїздів) і деяких – тільки одночасно для обох підсистем (параметри загального фундаменту), тобто в такому об'єкті присутні всі перераховані вище види зв’язності. Все це істотно впливає як на моделі, використовувані в керуванні проектами та програмами будівництва, так і на вибір математичних методів керування, зокрема, оптимізації [9]. 

 Сьогодні цей вибір досить обмежений. Так, наприклад, у цей час існують методи комплексної еволюційної оптимізації [10], однак вони призначені тільки для об'єктів із сильнозв’язаними параметрами підсистем. Те ж можна сказати й про інші методи оптимізації складних об'єктів в УП.

 Зв’язність підсистем у випадку будівельного об'єкта повністю визначається інфраструктурою об'єкта [10]. Ці зв'язки, як і у будь-яких інших багатоелементних системах, можуть носити детермінований, стохастичний, а також нечіткий характер, надаючи менеджерові проекту широкі можливості при побудові моделей такого процесу і виборі методу його оптимізації.

 Інфраструктура будівельного об'єкта – поняття досить широке, тому в роботі виділяли її природну складову (рельєф місцевості, стан ґрунтів, троянду вітрів, природні водойми й т.д.) і штучну складову (згадані вище штучні мережі, дороги, стан висвітлення й т.п.).

 Запропоновані методи та моделі є новими развитиями теорії оптимізації проектних рішень у будівництві, зокрема, уперше запропоновано розділити модель інфраструктури об'єкта на дві зв'язані підмоделі, у кожній з яких еволюційна оптимізація здійснюється автономно, але з обліком сильної або слабкої зв’язності їхніх параметрів. 

 На прикладі простої системи, у якої цільова функція z залежить тільки від двох аргументів: x й y, розглянемо відмінності в підходах до оптимізації об'єктів, що містять різні по зв’язності підсистеми.

 Об'єкти, що містять тільки незв'язані підсистеми. Нехай деяка система (об'єкт, пристрій, конструкція) А складається із двох підсистем А₁ й А₂, однозначно обумовлених парами аргументів х₁, в₁ і х₂, в₂, відповідно, у вигляді точок на мал. 3 а. При цьому виконуються обмеження: 0 ≤ x₁ ≤ x_max, 0 ≤ y₁ ≤ y_max, 0 ≤ x₂ ≤ x_max й 0 ≤ y₂ ≤ y_max. Тому що підсистеми А₁ й А₂ незв'язані, то в процесі оптимізації кожна з них може вільно переміщатися в зоні обмежень, змінюючи разом з «своїми» аргументами x й y також «свою» цільову функцію z:

z_i = z (xi, yi); i = {1, 2}.           (1)

 

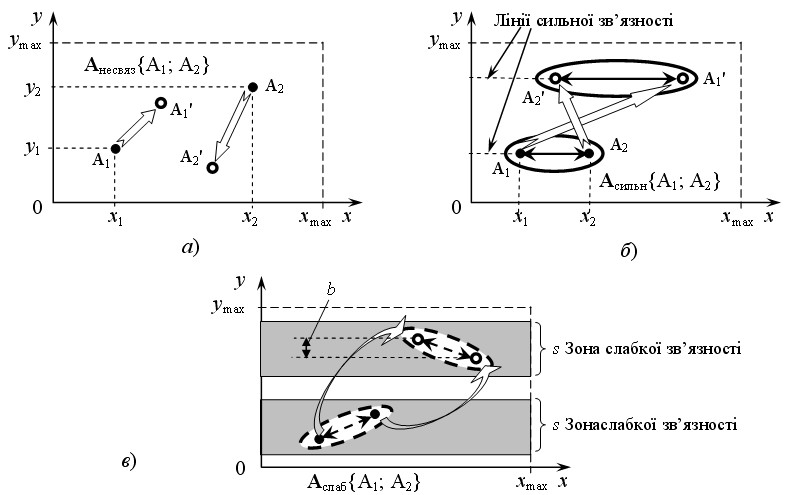
 Мал. 3. Схеми траєкторій можливих переміщень аргументів незв'язаних (а), сильнозв’язаних (б) і слабозв’язаних (в) підсистем у процесі оптимізації

 

 У цьому випадку відсутність зв'язку приводить до того, що сукупність підсистем А₁ та А₂ втрачає системні властивості: кожна підсистема може піддаватися оптимізації шляхом підбору (розрахунку) аргументів без якої-небудь «оглядки» на іншу.

 Об'єкти, що містять тільки сильнозв’язані підсистеми. У роботі [11] описані об'єкти, що володіють додатковим твердим обмеженням на зміну проекту конструкції в процесі оптимізації: одна зі змінних (наприклад, y) є узагальненою в тому розумінні, що завжди має місце співвідношення (мал. 3 б):

y₁ = y₂.    (2)

 Зазначимо, що величини y₁ та y₂ можуть змінюватися, але тільки одночасно, так, щоб не порушувалося співвідношення (2) (мал. 3 б).

 Об'єкти, що містять тільки слабозв’язані підсистеми. У дійсній роботі розглядаються об'єкти, у яких властивість (2) менш тверде: 

 У цьому випадку відхилення аргументів y₁, y₂ друг від друга допускаються, але тільки на величину b, що лежить у межах деякої зони зв’язності s.

 При стохастичному характері розподіл імовірності відхилень по перетині зони зв’язності залежить від властивостей об'єкта та умов його експлуатації. Нехай р_b – імовірність того, що величина b = ± (y₂ – y₁) прийме значення y з діапазону 0 ≤ y₂ – y1 ≤ s, де s – ширина зони зв’язності в одиницях, у яких виміряється узагальнений параметр y. При оптимальному проектуванні зона зв’язності може переміщатися, змінювати свою ширину s, що також є випадковою величиною, але слабозв’язані елементи будуть завжди залишатися усередині її (мал. 3 в). 

 Аналіз об'єкта оптимізації з метою виділення підмножин його параметрів: аргументів з різною зв’язністю та цільової функції розглянемо на конкретному простому прикладі. 

 Зокрема, для нашого приклада параметри системи, що враховують у процесі оптимізації процесу керування програмою будівництва комплексу будинків і споруджень, наведені в табл. 1.

Таблиця 1

Параметри системи, що враховують у процесі оптимізації

 

 Як видно з таблиці, навіть у найпростішому випадку керування програмою існують параметри оптимізації, що відносяться до перерахованого вище, що відрізняються формою зв’язності елементів підсистем.

 В умовах багатопараметричності, багатоекстремальності та багатокритеріальності процесу керування програмою будівництва різнотипних комплексів із зв’язаними параметрами найкращим методом оптимізації представляється еволюційний генетичний алгоритм, перетворений під роботу зі складнозв’язаними системами [12]. 

 Запропоновано методи й моделі оптимізації параметрів керування проектом будівництва споруджень, засновані на обліку зв’язності між характеристиками підсистем об'єкта оптимізації.

 Результати дослідження рекомендуються для використання в організаціях, що здійснюють проектний менеджмент в області будівництва різнотипних комплексів із зв’язаними параметрами, а також у навчальних закладах відповідного профілю. 

 

Литература

1. Березіна, С. В. Системи екологічного управління [Текст] : Довідниковий посібник з впровадження міжнародних стандартів серії ISO 14000 / С. В. Березіна. – К. : Aiva Plus Ltd, 2009. – 62 с.

2. Бібік, Н. В. Екологічне будівництво як інноваційний підхід формування сталого розвитку України [Текст] / Н. В. Бібік // Економіка будівництва і міського господарства. – 2014, ТОМ 10, НОМЕР 1, 23–29.

3. Давиденко, В. А. Ландшафтна екологія. Навчальний посібник [Текст] / В. А. Давиденко, Г. О. Білявський, С. Ю. Арсенюк. – К. Либра, 2007. – 280 с.

4. Бахрушин, В. Е. Слабосвязанные системы в природе и обществе [Текст] / В.Е. Бахрушин // Складні системи і процеси. – 2003. – № 1. – С. 21 – 25. 

5. Становский, А. Л. САПР электротехнического оборудования со слабосвязанными элементами [Текст] / А. Л. Становский, П. С. Швец, А. В. Торопенко // Сучасні технології в машинобудуванні: збірник наукових праць. – 2013. – Вип. 8. – Харків, НТУ «ХПІ». – С. 133 – 143.

6. Перпері, А. О. Модернізація математичного методу генетичного алгоритму для оптимізації геометрії шліфувальних кіл [Текст] / А. О. Перпері, П. С. Швець, Д. А. Монова // Вісник Одеської державної академії будівництва та архітектури. – 2011. – № 41. – С. 217 – 221.

7. Становский, А. Л. Эволюционная оптимизация слабосвязанных технических систем в САПР [Текст] / А. Л. Становский, П. С. Швец, Д. А. Желдубовский // Праці Одеського політехнічного університету: Науковий та науково-виробничий збірник. – 2011. – Вип. 2(36). – С. 234 – 238.

8. Становский, А. Л. Оптимизация слабосвязанных систем в автоматизированном проектировании и управлении [Текст] / А. Л. Становский, П. С. Швец, И. Н. Щедров. – Сучасні технології в машинобудуванні: збірник наукових праць. – Вип. 6. – Харків, НТУ «ХПІ», 2011. – С. 129 – 134.

9. Дорошук, А. В. Применение современных методов для оптимизации электронных схем [Текст] / А. В. Дорошук // Труды Одесского политехнического университета. – 1999. – 2 (8). – С. 28 – 31. 

10. Монова, Д. А. Комплексный генетический алгоритм [Текст] / Д. А. Монова, А. А. Перпери, П. С. Швец // Праці Одеського політехнічного університету: Науковий та науково-виробничий збірник. – 2011. – Вип.. 1 (35). – С. 176 – 180. 

11. LEED is transforming the way we think about how buildings and communities are designed, constructed, maintained and perated across the globe [Електронний ресурс]. – Режим доступу : http:// www.usgbc.org/leed.

12. Духанина, М. А. Эволюционная оптимизация слабосвязанных систем [Текст] / М. А. Духанина, Е. Ю. Лебедева, П. С. Швец, Л. А. Одукалец // Збірник наукових праць Інституту проблем моделювання в енергетиці ім. Г.С. Пухова, Київ, 2013. – № 67 – С. 74 – 81.