Даль Наталя

викладач

ВП НУБіП України

«Ірпінський економічний коледж»

Ірпінь

 

  Анотація

  Практична спрямованість навчання математики – це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у студентів навичок самостійної діяльності математичного характеру. Прикладна спрямованість навчання математики формує у студентів розуміння математики як методу пізнання та перетворення оточуючого світу, який має розглядатися не тільки областю застосувань математики, а й невичерпним джерелом нових математичних ідей.

  Ключові слова

  Математика, навчальний процес, задачі практичного змісту, мотивація, заняття, студент.

 

  Одним із дієвих та ефективних засобів реалізації прикладної спрямованості курсу математики є використання в навчальному процесі прикладних задач, які виникли в інших галузях, але потребують математичного розв’язання.

  Використання прикладних задач під час вивчення математики є важливим аспектом свідомого сприйняття навчального матеріалу студентами, адже саме прикладні задачі викликають у студентів активізацію розумової діяльності, сприяють виникненню особистих мотивів навчання. Задачі, які містять нові відомості з різних життєвих галузей, розвивають інтерес і допитливість.

  Задачі практичного змісту потребують особливої уваги з боку викладача, тому що спочатку їх потрібно сформулювати мовою математики, тобто скласти математичну модель задачі. Це найбільш складна (і тому найбільш цінна для студентів) частина роботи. Для її виконання викладачу слід уважно підійти до кожної конкретної задачі: підготувати ряд евристичних запитань, що спрямують студентів до конкретного навчального матеріалу; визначити суттєві та абстрагуватися від несуттєвих властивостей об’єкта; сформулювати умову та вимогу прикладної задачі мовою математики.

  Для розв’язання задач практичного характеру, як правило, потрібні деякі додаткові довідкові дані. Доцільно не включати ці дані в текст задачі, даючи в такий спосіб студентам можливість відчути, що даних задачі недостатньо для її розв’язання, зрозуміти, яких саме даних не вистачає, і за можливості змусити їх самих відшукати ці дані в довіднику. Це також потребує особливої підготовки і викладача, і студентів.

  На таких заняттях підвищується активність студентів, а в результаті покращується якість запам’ятовування і відтворення досліджуваного матеріалу, оскільки студенти не тільки сприймають матеріал від учителя, а й самі беруть активну участь у його створенні та засвоєнні шляхом поєднання розумових операцій з практичними діями. Розв’язування задач практичного змісту сприяє розвитку творчої самостійності, ініціативи учнів, дозволяє краще реалізувати принцип зв’язку теорії з практикою.

  Прикладна задача повинна відповідати таким вимогам: питання задачі формулюється так, як воно зазвичай формулюється у житті; розв’язок задачі демонструє практичне застосування математичних ідей у різних галузях;

  Зміст задачі повинен викликати в учнів пізнавальний інтерес; дані та шукані величини задачі мають бути реальними, узятими з життя.

  Розв’язування прикладних задач сприяє ознайомленню студентів із роботою підприємств і галузей народного господарства, викликає інтерес до обраних професій.

  Використання прикладних задач дає можливість вдало створювати проблемні ситуації на занятті. Такі задачі забезпечують посилення мотивації навчання математики, спонукають студентів до здобуття нових знань, оволодіння новими вміннями, збагачують їх знаннями з інших дисциплін.

  У математиці задачі відіграють важливу роль. Iсторiя свідчить, що математика як наука виникла iз задач i розвивається в основному для розв'язування задач.

  Задачі стимулювали не лише виникнення, а й подальший розвиток математичної науки. Основну роль, звичайно, відігравали задачі, поставлені життям. Вони насамперед примушували вчених розробляти нові алгоритми, виявляти нові закономірності, створювати нові методи дослідження. Згадаймо, наприклад, історію виникнення диференціального та інтегрального числення. Ще на початку ХVІІI ст. математики зіткнулися з багатьма задачами на дослідження різних процесів, на знаходження площ криволiнiйних фігур, об’ємів тіл тощо. Ці задачі цікавили багатьох, вони послужили стимулом i вiдправним пунктом для створення диференціального та інтегрального числення. Так само задачі про азартні ігри привели до тeopiї ймовірностей. Задача на оптимальне завантаження верстатів привела до створення лінійного програмування i т. ін. I тепер математика розвивається в основному через розв'язування задач.

  Принцип навчання через розв'язування задач є очевидним наслідком iз самої природи математики. Розв'язування задач – найефективніша форма не тільки для розвитку математичної діяльності, а й для засвоєння знань, навичок, методів і застосувань математики.

  Не потрібно відокремлювати вивчення тeopii вiд розв'язування задач. Ці два види роботи повинні переплітатися i обумовлювати один одного.

  У багатьох випадках задачі практичного змісту можна застосовувати для мотивації навчальної діяльності студентів перед вивченням нового матеріалу, для створення перед вивченням нової теми так званої проблемної 

  На прикладі добре складених задач прикладного змісту студенти переконуються у значенні математики для різноманітних сфер людської діяльності, в її користі i необхідності для практичної роботи, бачать широту можливих застосувань математики, зрозуміють її роль в сучасній культурі.

  Задачі на складні відсотки

  Задачі на складні відсотки розв'язуються в досить швидкий спосіб при знанні декількох простих формул. Частина з них стосується нарахувань по внеску чи кредиту, коли ті здійснюються за певні часові проміжки. Також складні відсотки використовують в задачах хімії, медицини та ряді інших.

  ФОРМУЛИ СКЛАДНИХ ВІДСОТКІВ

  У випадку розміщення вкладів з капіталізацією відсотків на роки кінцева сума депозиту визначається формулою 

 

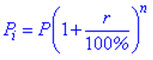
  Тут P – початковий внесок, r – відсоткова ставка, n – кількість років. За складними відсотками працюють банки, івестиційні фонди, страхові фірми. Поширені за кордоном, а зараз і в Україні – пенсійні фонди та фонди страхування життя працюють за схемою складних відсотків. При розміщенні вкладів з капіталізацією відсотків поквартально формула складних відсотків матиме вигляд

 

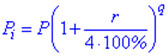
  де q – кількість повних кварталів.

  При капіталізації відсотків щомісячно застосовують наступну формулу для обчислень

 

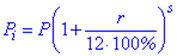
  де s – кількість місяців існування угоди.

  Останній випадок, неперервне нарахування відсотків, коли складні відсотки нараховують щоденно, розраховують за формулою

 

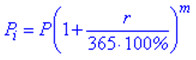
  де m – кількість днів.

  Страхування життя та відкладання пенсій відбувається за складнішими формулами, крім нарахування складних відсотків щороку здійснюються необхідні внески.

  Розглянемо два випадки накопичення. Чоловік відкладає 5000 грн. протягом 20 років. За цей час він відкладе 20*5000=100000 (грн).

  При відкладанні у накопичувальні фонди з річною ставкою 13%, за перший рік сума зросте до 5000*(1+13/100)=5650 (грн)

  Наступного року чоловік до даної суми додає ще 5000 грн. В результаті, за другий рік сума збільшиться 

  (5650+5000)*(1+0,13)=12034.50 (грн)

  Продовжуючи подібні обчислення, вкінці терміну отримаємо суму розміром 457349,58 грн.

Поширені задачі на складні відсотки

  Задача 1. Вкладник поклав на депозит $3000 під 9% річних на 10 років. Яка сума акумулюється наприкінці 10-го року при річній капіталізації? На скільки зросте сума порівняно з початковим внеском?

  Розв'язання:

  Застосовуємо формулу складних відсотків для знаходження суми наприкінці терміну

 

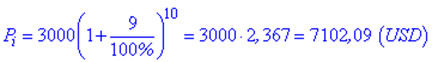
  Щоб дати відповідь на друге питання, від значення 7102,09 віднімаємо суму вкладу.

   Різниця становить 4102 долари. 

  Задача 2. Інвестор вклав 7000 грн під 10% річних при умові нарахування складних процентів щокварталу. Яку суму він отримає через 8 років?

  Розв'язання: 

  Застосовуємо 2 формулу складних відсотків.

  Знаходимо кількість кварталів   

  та підставляємо у формулу

 

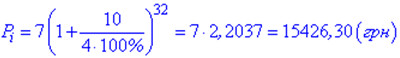
  Задача 3. Костюм коштував 600 грн. Після того як ціну було знижено двічі, він став коштувати 432 грн., причому відсоток зниження вдруге був у 2 рази більшим, ніж першого разу. На скільки відсотків кожного разу знижувалася ціна?

  Розв'язання: 

  Для спрощення обчислень позначимо 

  X – перша знижка; 

  X/2 – друга знижка;

  Щоб відшукати невідому X складаємо рівняння

 

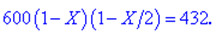
  Спрощуємо, та зводимо до квадратного рівняння

 

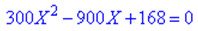
  та розв'язуємо

 

 

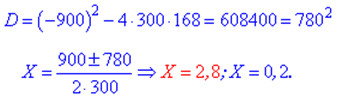
  Перший розв'язок не має фізичного змісту, другий враховуємо при обчисленнях. Значення 0,2 відповідає зниженню на 0,2*100%=20% після першої знижки, та X/2 =10% після другої знижки.

 

Література

1. Г.М.Возняк. Взаємоз’вязок теорії з практикою в процесі вивчення математики. Київ. 1989р.

2. А.А.Окунев Спасибо за урок, дети!: о развитии творч.способностей учащихся: Кн. для учителя: Из опыта работы.– М.: Просвещение, 1988.

3. Горох О.О. Комп’ютер на уроці математики. // Математика. – 2007. - № 2.

4. Зімановська А.А. Проведення практичних робіт з математики. // Вісник. – 2008. 

5. Науково-методичні основи використання лабораторних робіт в процесі викладання математики. – http:// www.allbest.ru 

6. Теоретичні основи проведення практичних робіт на уроках математики. – http://www. school3207.ucoz.ru