УДК 621.382
Амірова Марія Владиславівна
Магістрант Одеського національного політехнічного університету(ОНПУ)
Україна, м. Одеса
Анотація: в даній роботі описаний метод кластеризації на базі мультістартової оптимізації з використанням вейвлет-перетворення і представлені розрахункові дані для різних ітерацій і кроку дискретизації.
Ключові слова: кластеризація, класифікація, мультістартова оптимізація, вейвлет-перетворення.
Сучасний етап розвитку радіоелектроніки і телекомунікаційних систем характеризується загостренням проблеми надійності та якості в цілому внаслідок ускладнення радіоелектронної апаратури (РЕА), що виражається як у різкому збільшенні кількості використовуваних елементів і блоків, в появі якісно нових відповідальних функцій, покладених людиною на апаратуру, так і в ускладненні умов роботи. В силу цих причин підвищуються вимоги до точності і ефективності виконання заданих функцій не тільки системою в цілому, а й кожним окремим елементом. Наприклад, у найбільш жорстких умовах повинна функціонувати радіоелектронна апаратура (РЕА), встановлена на атомних станціях.
Найбільш достовірні і повні показники надійності зазвичай отримують за результатами експлуатації апаратури. Однак ця інформація надходить, як правило, з великим запізненням. Традиційні методи випробувань апаратури в багатьох випадках також не дозволяють підтвердити заданий рівень її надійності і якості через наявність ряду прихованих дефектів. У зв'язку з цим одним з перспективних напрямків у розробці ефективних і економічно прийнятних методів оцінки надійності та якості РЕА є передбачення їх майбутнього стану [1].
При отриманні прогнозних оцінок довговічності ІС можливі два підходи дослідження фізико-хімічних процесів, що протікають в елементах конструкції ІС (фізичні методи прогнозування) та математичне моделювання процесу деградації (методи статистичного прогнозування).
Згідно з даними зарубіжної літератури інтенсивність відмов ІС має бімодальний характер, а довговічність при екстраполяції до нормальної температури оцінюється величиною понад 100 тис. років. Однак в літературі відсутні дані по фактичної напрацювання ІС, що підтверджують достовірність прогнозів прискорених випробувань.
У ряді випадків досить не проводити прогноз для кожного компонента, а оцінювати, до якого класу (якісних або неякісних виробів) відноситься група (партія) таких виробів [2]. Це може бути актуально при виборі або налагодженні параметрів технологічного процесу виробництва.
Математична модель кластеризації.
Для передбачення параметрів важливою є класифікація з самонавчанням, яка складається з двох процедур: кластеризації та класифікації. При кластеризації визначають кількість і склад груп параметрів-ознак, при класифікації - будують поверхні, що розділяють ці групи в просторі ознак.
При кластеризації може бути не відомо кількість кластерів, кластери можуть мати складну форму і перетинатися, відрізнятися за розмірами і щільності. При класифікації з самонавчанням може бути не відомо кількість груп параметрів в просторі ознак і число образів в групах. У ряді завдань технічної діагностики серед параметрів необхідно виділити групи з загальними властивостями. Кількість таких груп (кластерів) і число виробів в них, як правило, невідомо.
Метод кластеризації на базі мультістартової оптимізації з використанням вейвлет-перетворення реалізується за схемою[2]:
c[n]=c[n-1] - ϒ [n]WTk (Q(x[n],c[n-1])) -1
де Q(x, c) – функціонал, залежить від вектору коефіцієнтів С = ( С1…, СN ) и от x = (x1 ,…, xM ); γ[n] – крок; n– номер ітерації; k– номер старту;
WTk(Q(x[n],c[n 1])) ={ G1k,G2k,…,GNk}
визначає напрямок руху до екстремуму:
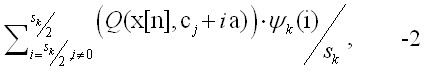
де Sk – довжина носія ВФ на k-м старті (Sk – парне число); a - крок дискретизації; Ψk(i) – ВФ на k-м старті (табл. 1); j = 1, …, N – розмірність вектору параметрів. Для оцінки напрямки пошуку оптимуму в обрані симетричні і нестаціонарні ВФ, на першому етапі - ВФ виду:
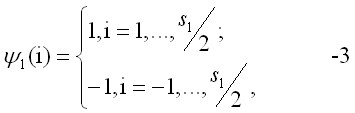
- на наступних етапах:
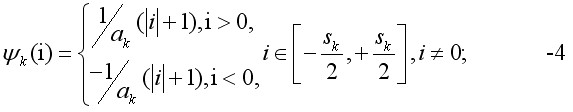
При ітеративному підході до кластеризації визначають оптимальний вектор координат центрів кластерів c=copt , який, задовольняючи обмеженням, доставляв би екстремальне значення Q(x,c) - функціоналу вектору С = ( С1…, СN ) залежить від вектору випадкових послідовностей x = (x1 ,…, xM ). за образам x ![]() X визначаються центри множин Xk та їх межі. При цьому
X визначаються центри множин Xk та їх межі. При цьому
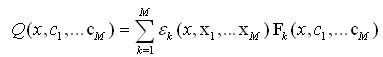
- реалізація функціоналу якості; Fk ( x,С1…, СM ) – функція відстані елементів x безлічі X від «центрів» ck підмножин Xk (кластерів); εk( ) - характеристичні функції,
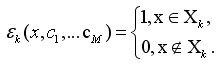
Таким чином формується метод кластеризації на базі мультістартової оптимізації з використанням вейвлет-перетворення. Створивши на основі цього методу програму можна розділити масив даних на два класи якісних і неякісних параметрів, тим самим відсікаючи браковані вироби на початковій стадії.
Вивчення впливу кроку дискретизації та ітерації на МОВП.
Для роботи були обрані інтегральні схеми ТТЛ ІС типу 106ЛБ1 за параметрами UOL (вихідна напруга низького рівня) і UOH (вихідна напруга високого рівня) [3]. Під технічними характеристиками ІС розуміють електричні параметри ІС, які підлягають контролю за технічними умовами (ТУ). Наприклад, для ТТЛ ІС обов'язковим є контролювання параметрів UOL (вихідна напруга низького рівня) і UOH (вихідна напруга високого рівня). Графічне зображення параметрів ІС при зміні зовнішніх умов представлено на гістограмі (Мал. 1)[3].
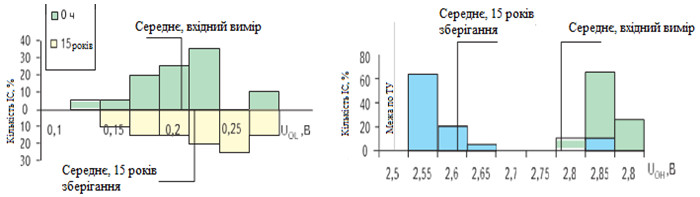
Малюнок 1 Параметри ІС при зміні зовнішніх умов.
Для дослідження було обрано метод кластеризації на базі МОВП, вибірка з 40 параметрами ІС у двовимірному просторі. Під час обробки параметрів за допомогою методу МОВП було знайдено центри кластерів С1 (0.1710; 2.6241) і С2 (0,2801; 0, 2903), а дані були розділені на 2 групи якісних (кола) і неякісних (квадрати) параметрів (Мал. 2).
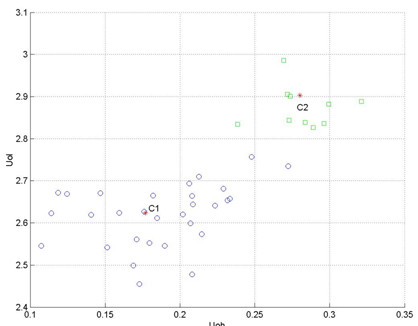
Малюнок 2 Реалізація кластеризації 40 параметрів ІС.
Проаналізуємо як змінюється час розрахунків від довжини носія (5…10), кроку дискретизації (0,1…0,4) та від кору ітерації (0,1...0,6).
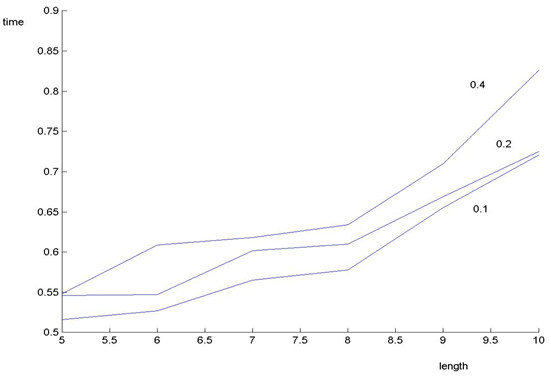
Малюнок 3 Залежність часу від довжини носія.
Крок дискретизації дорівнює 0,1; 0,2 ; 0,4.
З графіків видно, що час, який витрачає програма на розрахунки зростає зі збільшенням довжини носія. Зростання часу розрахунку так само пов'язаний з кроком дискретизації і ітерацією.
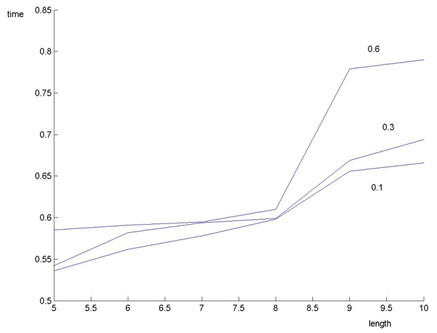
Малюнок 4 Залежність часу від довжини носія для ітерації 0,1; 0,3 ; 0,6.
При цьому, якщо розглядати залежність часу розрахунків від ітерації, то можна бачити, що в інтервалі від 6,5 - 8,25 лінії графіка наближаються одна до одної. Виходячи з цього можна зробити висновок, що час розрахунків для даних довжин відрізняється незначно. Це особливо яскраво виражено при L = 8. При перевищенні цього значення час розрахунків для великої ітерації значно зростає. Залежність часу розрахунків від кроку дискретизації має постійних характер для всіх довжин носія.
Висновки.
Для аналізу літературних даних необхідно і достатньо вибирати мінімальне значення кроку дискретизації і ітерації. Це дозволить оцінити вже існуючий прогноз за мінімальний час. При цьому для великих довжин носія збільшення ітерації хоч і дасть більшу точність, але потребує додаткових витрат часу. Даний метод хороший для оцінки надійності і якості РЕА за мінімальні терміни.
Література:
1. Строгонов А.В. Долговечность ИС и методы ее прогнозирования/А.В. Строганов//Автореферат Воронеж гос техн ун-т, 2006.
2. Щербакова Г. Ю. Субградиентный метод классификации в пространстве вейвлет-преобразования для технической диагностики / Г. Ю. Щербакова // Електротехнічні та комп’ютерні системи. - 2010. - № 1. - С. 136-142с.
3. Строгонов А.В. Использование нейронных сетей для изучения надежности ИС/А.В. Строганов//Компоненты и технологии 2006 №3.

