Паламар Олександра Сергіївна

магістрант 

Одеський національний політехнічний університет

Україна , Одеса 

  Анотація: задача даної роботи полягає в обґрунтуванні вибору типів реперних знаків для систем позиціонування та розрахунок ознак реперних знаків. У роботі проведено дослідження відносно вибору ознак реперних знаків для друкованих вузлів з поверхневим монтажем.

  Ключові слова: реперні знаки, позиціонування, інваріантні моменти, класифікація 

  Для забезпечення високої точності суміщення координатних систем автомата і друкованої плати необхідно виконання двох умов: поєднання не повинно бути механічним а базові елементи друкованої плати, що використовуються при поєднанні повинні бути частиною топології провідників , тобто виконані в одному з ними технологічному процесі при виготовленні друкованої плати. Такими елементами є реперні знаки. Реперний знак (РЗ) являє собою елемент топології провідників друкованої плати, що використовується як базовий при позиціонуванні компонентів в процесі їх установки.

  Практично в усьому сучасному технологічному обладнанні використовуються системи оптичного виявлення і контролю як компонентів при їх установці, так і реперних знаків. Цей факт в основному і визначає вимоги до реперних знаків: повинні легко розпізнаватись автоматизованими системами візуалізації на будь-якому технологічному обладнанні, легко відмінним від інших елементів топології і розташовуватися на платі таким чином, щоб бути видимим на будь-якому етапі автоматизованого поверхневого монтажу.

  При використанні автоматизованих систем візуалізації алгоритм поєднання систем координат друкованої плати і автомата такий: плата завантажується в автомат, відбувається її механічна фіксація. Потім система візуалізації шукає реперні знаки (мал.1) із заздалегідь певним розташуванням в системі координат автомата (з урахуванням допуску на похибку механічної фіксації). Визначаються реальні координати знайдених реперних знаків, відбувається обчислення різниці очікуваних і реальних координат реперних знаків. Потім здійснюється математичне зведення систем координат автомата і плати, тобто позиціонування [1].

  Для подальшої роботи ми обираємо 4 форми реперних знаків тому, що досліджуємо розпізнавання зображень ДВ з монтажем на поверхню. А для такого випадку найчастіше використовуються такі реперні знаки (мал.2)

Мал.2 Загальноприйняті форми реперних знаків для поверхневого монтажу

  Розпізнавання форм реперних знаків будемо виконувати на основі інваріанті моментів. Моментні характеристики знайшли широке застосування в багатьох задачах обробки цифрових зображень. Основна перевага моментних інваріантів є їх нечутливість до різних геометричних перетворень (зрушення, поворот, масштабування). Момент- це характеристика контуру зображення, об'єднаний з усіма пікселями контур. Усі центральні моменти виражаються через звичайні за формулою [2]:

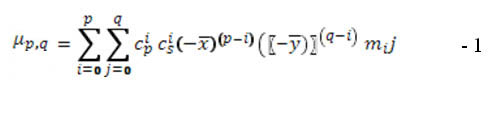
  Для реалізації інваріантності щодо масштабування центральні моменти нормують, що обчислюються наступним чином:

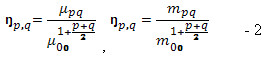
  Маючи всі ці моменти, можна визначити наступні сім інваріантних моментів, які інваріанті щодо переносів, осьової симетрії, поворотів, а також розтягнень і стиснень:

  У середовищі MatLab6.1 функція «invmoments» для обчислення інваріантних моментів є прямою реалізацію всіх цих формул. За допомогою команди f=imread(‘filename’) подали на функцію зображення. Після чого, завдяки команді phi=invmoments(f) отримали вектор-рядок із 7 компонентами, куди записуються обчислені інваріанти для кожної із заданих фігур. Отримані результати приведені у табл.№ 1

Таблиця № 1 Отримані результати

  

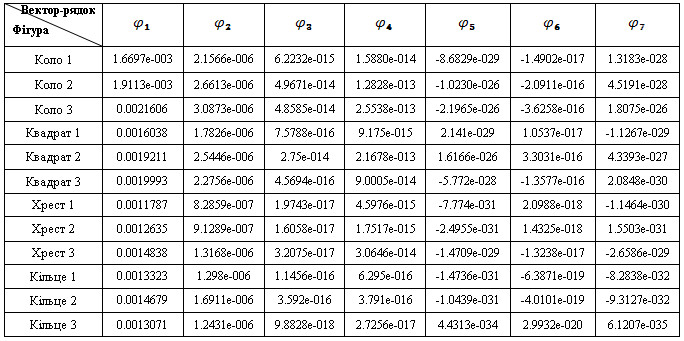
  Для подальшого виконання задачі класифікації необхідно обрати ті моменти ознак, які дозволять згрупувати об'єкти дослідження таким чином, щоб у просторі ознак класи різних об’єктів не перетиналися. В процесі дослідження для кожної пари груп ознак ми будували графік, де наочно можна було побачити розташування моментів ознак відносно один одного (наприклад коло і квадрат) і обрали ті моменти, кластери яких максимально різні між собою.

  У середовищі MatLab за допомогою команди plot(x,y) будуємо графіки залежностей для кожного з векторів      () кола і квадрата. Приклад реалізованих команд для першого вектору (  ) кола і квадрата (мал.3) :

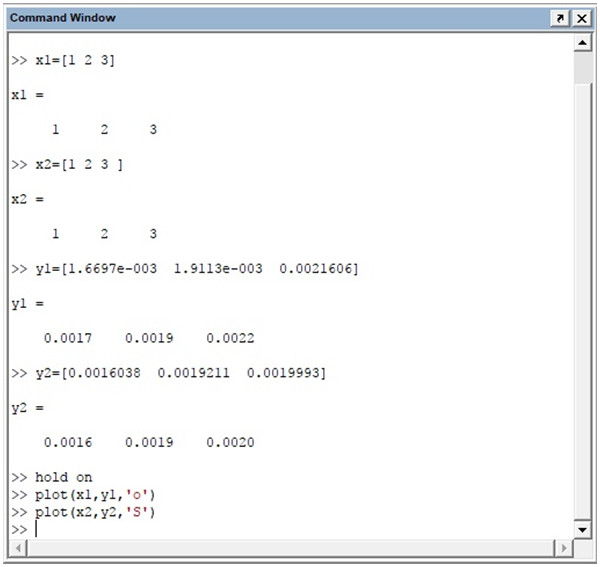
Мал.3. Приклад реалізованих команд для  кола і квадрата

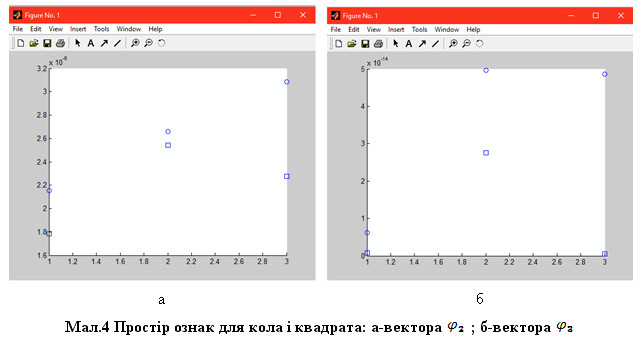
  Результати дослідження. Аналізуючи графіки просторового розташування для кожного з векторів, дійшли висновку, що у просторі ознак класи різних об’єктів (коло і квадрат) не перетинаються для   ,   (мал.4).

  У випадку з геометричною фігурою у вигляді кільця ми скористаємося програмою обчислення числа Ейлера. В середовищі MAtlab 6.1. за допомогою команди eul = bweuler(BW,n) обчислюється число Ейлера для фігури на бінарному зображені. Ця функція обчислює різницю між загальною кількістю об'єктів на зображені і кількістю отворів на них. Виходячи з цього можна дійти висновку, що кільце має суттєву відмінність від інших форм реперних знаків ,оскільки для нього число Ейлера буде дорівнювати 0.

  Можна зробити висновок ,що розпізнавання образів незалежно від позиції, орієнтації і розміру може бути досягнуто, використовуючи інваріанти моментів, які дозволяють згрупувати об'єкти дослідження таким чином, щоб у просторі ознак класи різних об’єктів не перетиналися.

Література:

1.Пивненко В.В.Реперные знаки, как неотъемлемый элемент успешного дизайна печатных плат//Технология и конструирование в электронной аппаратуре.-2007.-№6(47).-С.61-66.

2. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB// Радиоэлектроника.-2006.-С.490-493.