Дараган Тарас Геннадійович

студент 2 курсу магістратури

ДВНЗ «Донецький національний технічний університет»

Україна, м. Покровськ

  Анотація: В роботі розглянуто нові підходи до оптимізації комунікаційних операцій при чисельному розв’язанні задачі Коші для систем звичайних диференційних рівнянь з використанням паралельних блокових методів. Описано загальні проблеми, які виникають при обчисленні СЗДР паралельними блоковими методами з використанням багатопроцесорних комп’ютерів та кластерів, а саме, розподіл обчислювального навантаження на усі процесорні елементи. Запропоновано нові підходи для ефективного розподілу навантаження на доступні процесори. За допомогою реалізованої програмної системи проведено дослідження запропонованих методів, а також наведено результати дослідження ефективності цих методів.

  Ключові слова: чисельні методи, паралельне моделювання, блокові методи, комунікаційні операції, керування кроком, MPI

  Найбільша потреба в ефективних паралельних методах виникає при моделюванні динамічних об'єктів з зосередженими параметрами, які описуються системами звичайних диференціальних рівнянь. Головною перешкодою до впровадження практично всіх паралельних систем є відсутність ефективних прикладних паралельних методів. 

  Мета роботи полягає в дослідженні і розробці алгоритмів керування кроком і порядком інтегрування при вирішенні жорстких систем на основі паралельних коллокаційних блокових методів [1] з генеруванням коефіцієнтів методу заданого порядку точності для отримання максимальної реальної продуктивності.

  Неявні колокаційні методи, зазвичай мають, абсолютну стійкість, що дозволяє використовувати їх при вирішенні жорстких задач [2], але з цим зростає складність побудови на їх основі алгоритмів автоматичної зміни розміру кроку інтегрування. Головна ідея блочних методів полягає в одночасному отриманні наближень точних розв’язань в рівновіддалених точках блоку, однак це унеможливлює зміну кроку всередині блоку. Колокаційні методи для розв’язання задачі Коші будуються на інтерполяційних многочленах, причому їх ступені збігаються з кількістю точок колокації, тому значення багаточленів в цих точках збігаються з правими частинами диференціального рівняння в розрахункових точках. У випадку, коли розрахункова функція характеризується різною швидкістю зміни на окремих ділянках інтегрування, застосовують схему, де до розрахункового блоку вводяться додаткові точки. Розрахунки в таких блоках можуть виконуватись паралельно, а обмін розрахованими значеннями буде проходити лише після розрахунку усіх точок у блоках (рис. 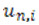1), де   - наближені значення розв’язання задачі Коші в точках   , i = 0,1,2..s.

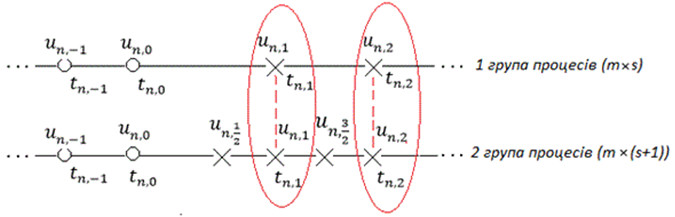
Рисунок 1 – Дві паралельні нитки обчислень m-крокового s-стадійного блокового методу 

  Звичайна реалізація такої схеми, з використанням технології MPI має на увазі, що кількість доступних процесорів розподіляється на дві групи, де за кожною із груп закріплюється одна нитка обчислювань, а за кожною стадією в блоці закріплюється окремий процесор, який вираховує на одній точці (стадії) усю систему рівнянь ЗДР. Після розрахунку усі процесори мають обмінятися своїми значеннями з усіма другими процесорами. Однак можуть виникати такі ситуації, коли число доступних процесорів більше за число стадій в двох блоках, і тоді рівномірний розподіл числа процесорів на дві групи може бути неефективним, тому що деякі процесори також будуть брати участь у обміну «усі з усіма», витрачаючи час на недоцільні операції обміну. Тому для оптимізації комунікаційних операцій було запропоновано два підходи для оптимального використання процесорів. 

  Перший підхід пропонується для використання на багатопроцесорних комп’ютерах, який полягає у наступному: так як в першому блоці число стадій може бути менше, ніж число стадій у другому розрахунковому блоці, то число необхідних процесів для першої групи потрібно також скоротити до числа стадій у першому розрахунковому блоці. Потім процеси, що залишилися, за такою ж схемою розподіляються і для другої групи, і тоді незадіяні процесори просто не будуть приймати участі у розрахунку. Такий підхід доцільно використовувати на архітектурі, яка описується топологією кільце. 

  Другий підхід розрахований для використання на багатопроцесорних кластерах, де мінімальне число доступних процесорів може перевищувати 100, тому при використані таких обчислювальних ресурсів доцільніше буде задіяти усі доступні процесори. Клас задач, які обчислюються блочними методами характеризується великою розмірністю системи, яка може досягати і 1000, і 10000 рівнянь. Тому обчислення усіх рівнянь на одному процесі не є ефективним, з точки зору часу виконання. Розподіл процесів на дві групи виконується за такою схемою: усі доступні процеси рівномірно поділяються на загальне число стадій у першому та другому розрахункових блоках так, щоб за кожною стадією було закріплено підгрупу процесів, приблизно однаковою розмірністю. Саме такій підхід дозволить додатково розпаралелювати обчислення всіх рівнянь системи на кожній стадії серед процесорів у кожній підгрупі. Таким чином при великій розмірності системи будуть задіянні всі доступні процеси.

  Для дослідження ефективності запропонованого першого підходу була розроблена програмна система з використанням технології MPI, в якій реалізовано модифікований алгоритм розподілу процесорів на дві групи, а також було реалізовано метод для обміну повідомленнями між паралельними процесами (рис.2).

Рисунок 2 – Фрагмент коду алгоритму розподілу процесорів та методу передачі повідомлень між паралельними процесами

  При проведені тестування обчислювалась задача Капса [3] блоковими методами з відомими точними розв’язаннями. Були проведені обчислення послідовним алгоритмом; паралельним алгоритмом зі стандартною схемою та модифікованою на 4, 6 та 8 процесах, результати яких зображені на рис. 3. 

  Тестування програмної системи виконувалося на комп’ютері з 4 доступними процесами, тому результати тестів, в яких задане число обчислювальних процесів 6 і 8, не відображають реальний час обчислення, що пов’язано зі специфікою використання потоків операційною системою. Однак аналіз результатів досліджень вказує на те, що запропонований модифікований метод оптимізації комунікаційних операцій керування кроком в паралельних алгоритмах моделювання з використанням багатопроцесорного комп’ютера ефективніше, ніж метод із загальною схемою паралельного алгоритму. Зведені дані результатів проведених обчислень відображені в табл. 1.

 Таблиця 1

Результати проведених обчислень

Рисунок 3 – Діаграма ефективності проведених обчислень на 6 та 8 процесах

Література

1. Дмитриева О.А. Коллокационные блочные методы с контролем на шаге // О.А. Дмитриева [Електронний ресурс]. — Режим доступу: http://www.hups.mil.gov.ua/periodic-app/article/12220/soi_2015_5_20.pdf

2. Параллельные численные методы моделирования динамических объектов: монография / О.А. Дмитриева. – Красноармейск: ГВУЗ «ДонНТУ», 2016. – 384 с.

3. Numerical Solution of Extended Block Backward Differentiation Formulae for Solving Stiff ODEs / [S.A.M. Yatim, Z.B. Ibrahim, K.I. Othman, M.B. Suleiman] //Proceedings of the World Congress on Engineering. WCE 2012, July 4 – 6, 2012, London, U.K. – 2012. – Vol. 1. – P. 109–113.