Шатохина Н.К.
кандидат технических наук, доцент
Османов В.С.
магистрант кафедры ПМИ
Донецкого национального технического университета
Решением задачи индуктивного обобщения является построение продукционной базы знаний (совокупность минимальных наборов высказываний в виде ДНФ).
Задачей индуктивного обобщения (ИО) является минимизация суждения экспертов в более общие суждения, из которых, выводились все верные высказывания экспертов. А также полученное множество было непротиворечивым, далее характеристическим (ХИО).
В качестве исходных данных выступают типы и характеристики фактов и коэффициентов уверенности, составляющие нечеткие продукции.
Синтаксис языка представления знаний. Пусть задано множество U (универсум) и непересекающееся с U множество Y. Элементы U называются элементарными фактами или атомами и обозначаются малыми буквами из начала латинского алфавита (a, b, c,…), а элементы Y - целевыми фактами, обозначим через x, y и т.д. Произвольные подмножества U обозначим большими буквами из конца латинского алфавита (W, Q, Z,…).
Формулой (продукционным правилом) называется выражение вида 
, где W - некоторое подмножество U, 
, а h - некоторый числовой коэффициент, называемый коэффициентом уверенности (КУ), и 0<h≤1.
Содержательно элементарные факты соответствуют различным элементарным высказываниям экспертов о предметной области (ПО), а формула ({a, b, c, d} 
y, h) понимается как «если имеет место a и b и с и d, то с уверенностью h можно считать, что выполняется y» [1].
Формулами БЗ описываются знания о взаимосвязи между элементарными и целевыми факторами, например, если «состояние атмосферы - солнечно, и температура воздуха - высокая, и влажность воздуха - низкая, и ветрено, то с достаточно большой уверенность (0,7) можно сказать, что погода хорошая», т.е. ({a, b, c, d} x, 0,7).
Если факт имеет истинное значение, то в продукции под соответствующей буквой записывается «1», иначе «0».
Семантика языка. Отдельная формула языка задает некоторую закономерность, которая в зависимости от состояния ПО формально описывается понятием интерпретации - нечеткое множество I=({a, µa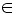}), a 
U, µa 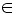[0, 1]. Каждое a соответствует некоторому высказыванию о состоянии ПО, a µa - степени уверенности в этом высказывании. То состояние ПО, для которого данная закономерность справедлива, описывается понятием модели соответствующей формулы.
Моделью формулы ({a1, a2,…, an}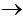 y, h) называется такая интерпретация I=({a, µa}), для которой выполняется условие µy≥min(µa1,…, µan, h). В частности, при n=0 µy≥h.
Под базой знаний (БЗ) понимается некоторое конечное множество формул. При этом предполагается, что БЗ описывает те состояния ПО, в которых одновременно выполняются все составляющие БЗ формулы. Иными словами, множество моделей БЗ является Mod (T) = ∩ Mod (fi) по всем fi 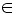T.
Формула f является логическим следствием БЗ T(T|-f), если M(T) 
M(f), т.е. логическими следствиями БЗ являются те формулы, которые выполняются всегда, когда выполняются все формулы БЗ.
Для принимаемого языка будем использовать следующую систему правил вывода:
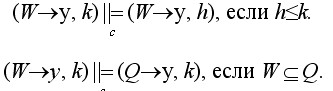
Каждое правило формулируется с одним целевым фактом y, поэтому можно рассматривать множество продукций для каждого целевого факта отдельно - (W,k).
Метод построения индуктивного обобщения
Рассматривается множество продукций Е –{w,h[i]}. Далее зафиксируем слой продукций с одним коэффициентом уверенности k: E(k).
Построим семейство множеств (w-V[i]), где V[i] принадлежат слоям k>l.
Представим (w-V[i]) в виде дизъюнкции.
Построим конъюнкцию (w-V[i]) для всех слоев k;
Преобразуем в ДНФ X(w)= (b1 
b2…. bn). Таким образом, каждая конъюнкция bi из Х(w) выводит (w,k) и не выводит ни одну (V[i],l), где l<k. Также для слоя E(k) подмножество Х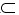 
X(w) – должно быть минимальным.
Для каждой продукции слоя k строим матрицу, где 0 соответствует отсутствию дизъюнкции в ДНФ, а 1 – присутствию в ДНФ.
Затем решаем задачу о покрытии таким образом, чтобы каждый слой k содержал минимальное количество продукций с минимальным количеством дизъюнкций.
Пошаговый пример работы метода с заданным набором продукций приведен в таблице 1.
Таблица 1
Начальные данные метода
|
|
a |
b |
c |
d |
E |
k |
|
W11 |
1 |
|
1 |
|
|
0.6 |
|
W12 |
|
1 |
|
1 |
|
|
|
W21 |
|
|
1 |
1 |
|
0.7 |
|
W22 |
1 |
|
|
1 |
1 |
|
|
W31 |
1 |
1 |
|
|
1 |
0.8 |
|
W32 |
|
1 |
1 |
|
1 |
1)
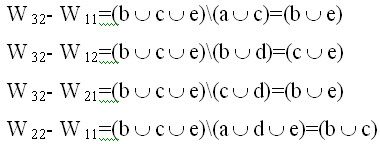
ДНФ 
Для {W32, 0.8} получено ИО(W 32) = ({bc},0.8);({eb},0.8);({ce},0.8).
2)
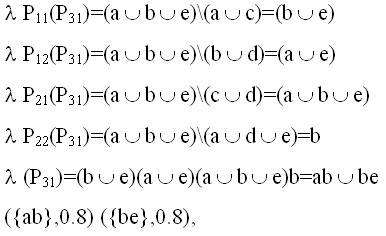
Для слоя Е(0.8) имеем ИО(0.8)= ({bc},0.8);({eb},0.8);({ce},0.8); ({ab},0.8).
Далее по аналогии выполняем следующие шаги.
3) ({ad},0.7);({e},0.7)
4) ({cd},0.7)
5) ({b},0.6);({d},0.6)
6) ({a},0.6);({c},0.6)
По множеству Е(0.8) строим матрицу (см. таблицу 2), в которой строки соответствуют продукциям Wki слоя, а столбцы – конъюнктивным членам mj из множества Е. На пересечении i-ой строки и j-го столбца находится 0, если конъюнктивный член mj отсутствует в ДНФ wki, а 1 – присутствует в составе ДНФ.
Таблица 2
Множество продукций слоя 0.8.
|
|
bc |
be |
ce |
ab |
|
W31 |
1 |
1 |
1 |
|
|
W32 |
|
1 |
|
1 |
После чего решаем задачу о покрытии строк (продукций), столбцами (конъюнктивными членами).
Метод построения индуктивного обобщения используя генетические алгоритмы
В качестве хромосомы рассмотрим двоичный вектор H={h1, h2, …, hn}, где hi =1, если конъюнктивный член включается покрытие продукций рассматриваемого слоя, hi =0 – в противном случае.
Нетрудно заметить, что 
, если Н содержит хотя бы один конъюнктивный член ДНФ продукции Wрi. Обозначим через,
Следовательно, задача сводится к следующему: вектор H={h1, h2, …, hn} является решением задачи, если 
и выполняется 
. В качестве фитнесс функции определим 
. В качестве решения в полученной популяции выбирается то, которому соответствует . Решение этой задачи можно осуществить, используя классические операторы генетического алгоритма – кроссинговер и мутацию [2,3].
В разработанном алгоритме построения индуктивного обобщения в качестве хромосомы используется факт с характерным ему коэффициентом уверенности. Таким образом, хромосомы группируются в разные слои, в зависимости от коэффициента уверенности.
Список литературы:
1. Грунский И.С., Шатохина Н.К. Об индуктивном обобщении нечетких заключений. Серія: Обчислювальна техніка та автоматика, випуск 25: Донецьк: ДонДТУ, ТОВ "Лебідь", 2001.-С.154-160.
2. Скобцов Ю.А., Скобцов В.Ю. Современные модификации и обобщения генетических алгоритмов //Таврический вестник компьютерных наук и математики. Симферополь: 2004, N1. – с.60-71.
3. Глазков Л.А. Генетические алгоритмы / Глазков Л.А., Куречик В.В., Куречик В.М. -М: Физматглит. – 2006.-319с.
