УДК 339.54:338:321(063):004

Булига Костянтин Борисович

кандидат технічних наук, доцент

Київський національний університет культури і мистецтв

місто Київ

Булига Олена Анатоліївна

Національний транспортний університет 

місто Київ

 

 Анотація: В статті запропоновано підхід до оптимальної організації митно-брокерських послуг з урахуванням можливості залучення додаткового персоналу. Об’єкт дослідження - зовнішньоекономічна діяльність транспортних підприємств. Мета роботи – розробити алгоритм оптимальної організації митно-брокерських послуг. Метод дослідження – математичний апарат теорії ігор. Організації, що займаються зовнішньоекономічною діяльністю мають в штатному розписі відповідну кількість митних брокерів, які здійснюють всі митні процедури. У випадку надзвичайних ситуацій, коли вони не встигають вчасно виконати митне оформлення, підприємство звертається до сторонніх спеціалістів. При цьому складається така ситуація: якщо звертатися заздалегідь, то вартість додаткових послуг одна, а у термінових випадках – інша. Використовуючи методи математичної теорії ігор можна оцінити переваги і недоліки того чи іншого підходу до залучення додаткових працівників. Розрахунки проводяться з використанням математичного процесора Mathcad.

   Ключові слова: митні процедури, теорія ігор, mathcad, вартість додаткових послуг, лінійний тренд

 

  Організації, що займаються зовнішньоекономічною діяльністю мають в штатному розписі відповідну кількість митних брокерів, які здійснюють всі митні процедури [1]. У випадку надзвичайних ситуацій, коли вони не встигають вчасно виконати митне оформлення, підприємство звертається до сторонніх спеціалістів. При цьому складається така ситуація: якщо звертатися заздалегідь, то вартість додаткових послуг одна, а у термінових випадках – інша. 

  Формалізуємо задачу: якщо впродовж доби митне оформлення не виконується, фірма несе збитки в розмірі ZB гр. Можна збільшити ймовірність оформлення до N%, якщо попередньо викликати стороннього брокера, вартість додаткових послуг в цьому випадку складає А1 гр. В терміновому випадку вартість додаткових послуг складає nА1 гр. Побудуємо математичну модель раціональної організації митного оформлення.

  Розіб’ємо задачу на наступні підзадачі:

  1) розрахунок кількості митних брокерів як каналів СМО при заданих інтенсивностях надходження і обробки заявок;

  2) прогнозування інтенсивності надходження заявок на основі попередньої статистики;

  3) розв’язання задачі оптимізації на основі результатів задач 1 і 2.

  1. Розрахунок кількості митних брокерів як каналів СМО

  Нехай інтенсивність надходження заявок на митне оформлення складає λ од/добу, а інтенсивність їх обробки kλ од/добу при умові  k>1. Змоделюємо за допомогою функції Mathcad [2] митне оформлення як систему масового обслуговування. На рис.1 показана залежність ймовірності простою системи від кількості каналів обслуговування при  k=1.1.

 

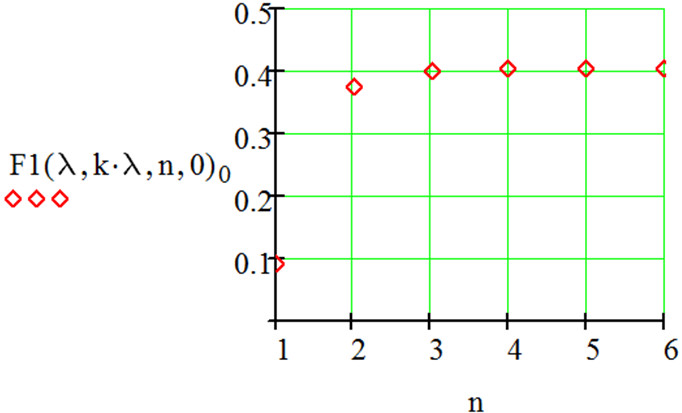
Рисунок 1- Залежність ймовірності простою системи від кількості каналів обслуговування при k=1.1

 

  З графіка видно, що при такому співвідношенні інтенсивності надходження і обробки, збільшення кількості каналів обслуговування з 2 до трьох і далі якісних змін не викликає.

  На рис.2 показана залежність ймовірності простою системи при одному (трикутні маркери), двох (хрестоподібні маркери) і трьох (квадратні маркери) каналах обслуговування від співвідношення інтенсивності надходження і обробки заявок при k∈ 1.1,...1.8

 

 

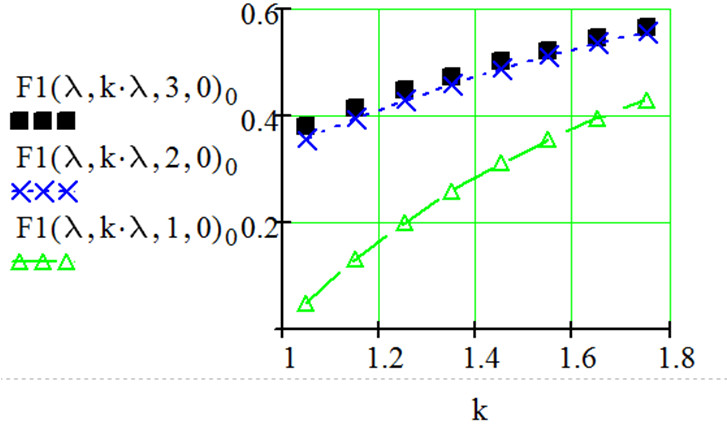
Рисунок 2 - Залежність ймовірності простою системи від співвідношення інтенсивності надходження і обробки заявок

  Аналіз розглянутих залежностей показує, якщо виконується умова k>1, наявність двох каналів обслуговування – двох митних брокерів - є оптимальною. Таким чином, планувати додаткові митно-брокерські послуги можна виходячи з наявної інтенсивності обробки заявок і прогнозу їх надходження. 

  2. Прогнозування інтенсивності надходження заявок

  При побудові трендів прогнозування найчастіше використовується лінійна залежність  . Зокрема, в системі Mathcad [2] лінійна апроксимація виконується за допомогою таких функцій

  • intercept(VX, VY) -  повертає значення коефіцієнта с₀;

  • slope(VX,VY) - повертає значення коефіцієнта с₁;

  • VX,VY -  вертикальні масиви, що задають відповідні значення х і у.

  На рис. 3 наведений приклад побудови лінійної апроксимації для довільного часового проміжку з 7 діб (тиждень). Масив VY задає відповідну кількість заявок, величина µ - інтенсивність обробки заявок. Величина VY- µ показує перевищення потоку заявок над інтенсивністю обробки. Використовуючи функцію  можна спрогнозувати можливу кількість заявок на наступні дні і відповідно приймати рішення про залучення додаткового персоналу до виконання митно-брокерських операцій.

 

 

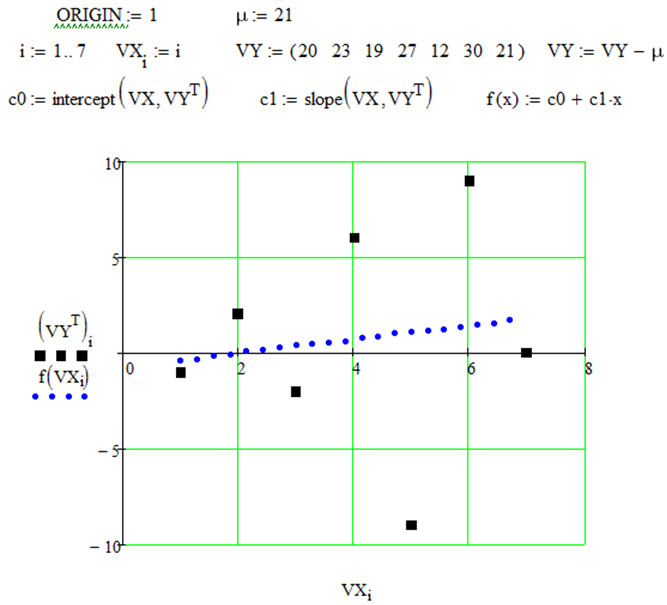
Рисунок 3 -  Побудова лінійного тренду надходження заявок на обробку

 

  В даному випадку тренд зростаючий, тому доцільно на найближчий термін залучати додатковий персонал.

  3. Загальна задача оптимізації витрат на митну обробку

  Нехай витрати на митну обробки без залучення додаткового персоналу складають А₀ гр., при вчасному замовленні додаткового персоналу маємо додаткові затрати А₁ гр., а при терміновому замовленні – nA₁ гр. Розглянемо випадкову величину витрат на митну обробку без залучення додаткового персоналу (табл.1), при вчасному замовленні додаткового персоналу (табл.2) і при терміновому замовленні (табл.3).

 

Таблиця 1 – Витрати на митну обробку без залучення додаткового персоналу

 

Таблиця 2 - Витрати на митну обробку при вчасному замовленні

 

Таблиця 3 - Витрати на митну обробку при терміновому замовленні

 

  Відповідні математичні сподівання складатимуть:

  

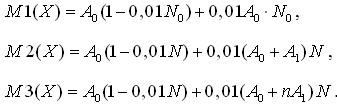
  Нехай прибуток від митного оформлення складає PR гр. за добу, а якщо впродовж доби митне оформлення не виконується, фірма несе збитки в розмірі ZB гр. 

  Розглянемо випадкову величину прибутку від митної обробки без залучення додаткового персоналу (табл.4), при вчасному замовленні додаткового персоналу (табл.5) і при терміновому замовленні (табл.6).

 

Таблиця 4 – Прибуток від  митної обробки без залучення додаткового персоналу

 

Таблиця 5 - Прибуток від  митної обробки при вчасному замовленні

 

Таблиця 6 - Прибуток від  митної обробки при терміновому замовленні

 

  Відповідні математичні сподівання складатимуть:

  

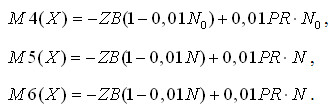
  Таким чином, маємо наступні варіанти дій фірми: 

  V₁ - не вживати ніяких додаткових заходів;

  V2  - заздалегідь залучити додатковий персонал;

  V3  - терміново залучити додатковий персонал.

  Їм відповідають два варіанти надходження заявок:

  U₁  - кількість заявок не перевищує можливостей обробки k>1;

  U₂   - кількість заявок перевищує можливості обробки k<1.

  Усього можливі 6 ситуацій, які описують всі комбінації з трьох стратегій фірми А та двох варіантів надходження заявок. Ці ситуації та супутні їм збитки і витрати наведено в табл. 7.

 

Таблиця 7 - Можливі середні денні витрати фірми 

 

  Вочевидь, перший варіант є найвигіднішим, а останній – найгіршим, але при цьому не враховуються ймовірності реальних ситуацій. Урахування статистичних даних можливе при обчисленні з використанням математичного сподівання та співвідношення між величинами А₀  і А₁, PR і ZB, а також значення коефіцієнта n. Розв’язання такої загальної задачі оптимізації в термінах теорії ігор не завжди можливо, тому в роботі пропонується порівнювати чисельні розрахунки для конкретних варіантів.  Для розрахунків таблиці 7 розроблено дві підпрограми-функції Mathcad, які дозволяють обраховувати показники в автоматичному режимі. 

 

Література:

1. Дмитриченко М.Ф. Основи теорії транспортних процесів і систем: [навч. посібник для ВНЗ] / М.Ф. Дмитриченко, Л.Ю. Яцківський, С.В. Ширяєва, В.З Докуніхін. –К.: ВД «Слово», 2009. –336 с.

2. Кирьянов Д. Самоучитель Mathcad 13 / Д. Кирьянов – СПб: БХВ-Петербург, 2006. – 528 с.