Булига Костянтин Борисович

кандидат технічних наук, доцент

Київський національний університет культури і мистецтв

місто Київ

Булига Олена Анатоліївна

Національний транспортний університет 

місто Київ

 

  Анотація: Многочлен Лагранжа узагальнено для випадку змінних координат внутрішніх вузлів. Для виводу відповідних формул застосовано математичний процесор Mathcad. Використання формул проілюстровано при виводі формул чисельного інтегрування.

 Ключові слова: Лагранж, змінні координати, чисельне інтегрування

 

  Розглянемо множники Лагранжа для випадку, коли проміжні точки інтерполяції є змінними. Так як будь-який відрізок можна за допомогою заміни координат привести до одиничного, то у подальшому в цьому розділі розглядатимемо відрізок t∈[0, 1]. Побудуємо коефіцієнти Лагранжа L20(t,a), L21(t,a), L22(t,a) для граничних вузлів t₀=0, t₂=1 та проміжного вузла із змінною координатою t₁ = a (0< a <1), а також коефіцієнти Лагранжа L30(t,a,b), L31(t,a,b), L32(t,a,b), L33(t,a,b) для граничних вузлів t₀ = 0, t₃ = 1 та проміжних вузлів із змінними координатами t₁ = a t₂ = b (0< a <1, 0< b <1, a < b). Для виконання алгебраїчних перетворень використаємо символічні операції expand (розкрити вираз) та simplify (спростити вираз)  системи MathCAD:

 

 Рис.1. Лістинг побудови множників Лагранжа

 

  Аналогічно можна отримати множники Лагранжа для будь-якої кількості проміжних вузлів. Побудуємо також коефіцієнти Лагранжа LG20(t,a,b,c), LG21(t,a,b,c), LG22(t,a,b,c) для трьох проміжних вузлів із змінними координатами t₀ = a, t₁ = b, t₂ = c (0<a<b<c<1):

 

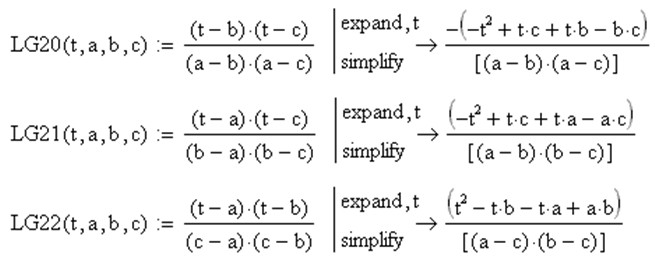
 Рис.2. Лістинг побудови множників Лагранжа для трьох проміжних вузлів

  Використовуючи Лагранжеві коефіцієнти із змінними координатами внутрішніх вузлів довільну функцію f(t) на відрізку [0,1] представимо многочленом Лагранжа:

 (1)

  Формули (1) використаємо для побудови квадратурних формул із змінними координатами внутрішніх вузлів. Для цього у визначеному інтегралі

 (2)

замінимо підінтегральну функцію многочленом Лагранжа (1).

   При n=2 маємо 

  (3)

  Якщо у формулі (3) покласти , то прийдемо до квадратурної формули Сімпсона [1].

  При n=3 маємо 

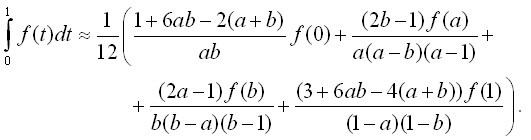  (4)

  Якщо у формулі (4) покласти , то прийдемо до квадратурної формули Ньютона («трьох восьмих») [1], якщо покласти 

 

то прийдемо до чотирьохточкової формули Маркова [1].

 При n=4 маємо 

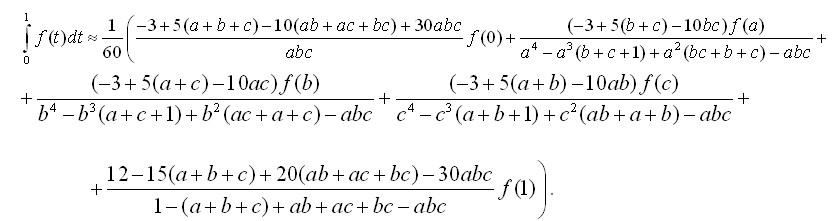  (5)

  Якщо у формулі (5) покласти , то прийдемо до п’ятиточкової формули Ньютона-Котеса [1], якщо покласти 

 

то прийдемо до п’ятиточкової формули Маркова [1].

  Визначимо похибку формули (2)

 (6)

Для цього розкладемо f(t) за формулою Тейлора, ділячи відрізок [0,1] на дві частини [0,a]  i [a,1] та приймаючи за центр розкладання точку t=a, 

 (7)

  Підставляючи розкладання (3.21) у формулу (3.20) та відкидаючи старші похідні, отримаємо 

 (8)

  Якщо у формулі (8) покласти , то отримаємо відому оцінку формули Сімпсона

 

  На рис. 3 наведено приклад обчислень у системі Excel за формулою (3) інтеграла 

 

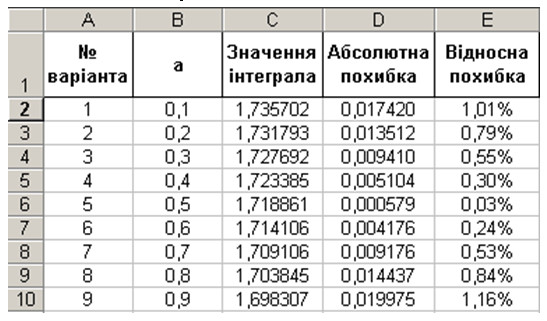
Рис. 3. Лістинг обчислень у системі Excel

  Як видно, відносна похибка не перевищує 1.2%, а найкращий результат відповідає формулі Сімпсона .

 

Література:

1. Бахвалов Н.С. Численные методы / Н. С. Бахвалов. – Москва: Наука, 1975. – 632 с.