Степовик Никита Сергеевич
студент-бакалавр кафедры энергетики
ГВУЗ «Украинский государственный химико-технологический университет »
Украина, г. Днепр
Коломиец Елена Викторовна
к.т.н., доцент кафедры энергетики
ГВУЗ «Украинский государственный химико-технологический университет »
Украина, г. Днепр
В данной работе, с допущением, что теплообмен между продуктами сгорания и насадкой, а также между воздухом и насадкой происходит только конвекцией разработана математическая модель насадочного регенератора тепла.
Ключевые слова: насадочный регенератор тепла, математическая модель, конвекция.
Насадочные регенераторы тепла нашли широкое применение в энергетике. Я планирую использование такого регенератора для подогрева воздуха идущего на горение при сжигании водоугольного топлива.
Целью данной работы есть разработка математической модели работы насадочного регенератора тепла.
Из-за малой величины объемов газа, находящихся между соседними частицами слоя, их излучением можно пренебречь. Поэтому принимаем, что теплообмен между продуктами сгорания и насадкой, а также между воздухом и насадкой происходит только конвекцией. Из-за малости диаметра шариков их можно считать термически тонкими телами. Таким образом, можно принять, что в каждой насадке происходит теплообмен в неподвижном слое, состоящем из термически тонких частиц. Тепловая работа насадки состоит из многократно повторяющихся циклов, включающих горячий (дымовой) и холодный (воздушный) периоды. Схема такой насадки показана на рис. 2.
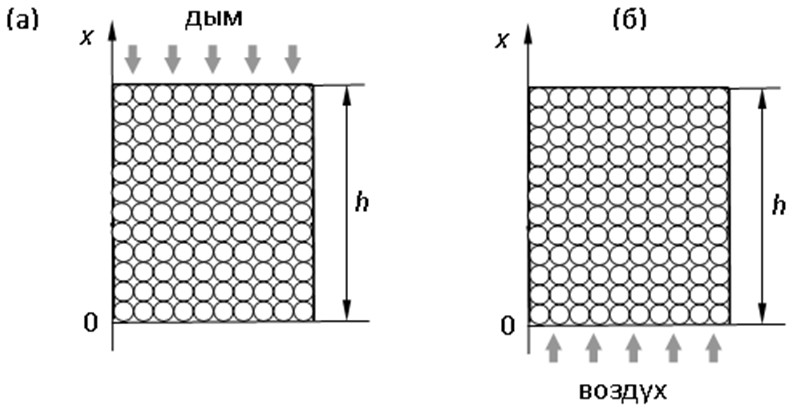
Рис. 1 – работы насадочного регенератора тепла Схема насадки регенератора в горячем (а) и холодном (б) периодах
Математическая постановка задачи для горячего (дымового) периода:
- дифференциальное уравнение теплообмена для слоя

- дифференциальное уравнение теплообмена для дыма

начальное и граничное условия

Для холодного (воздушного) периода:
- дифференциальное уравнение теплообмена для слоя

- дифференциальное уравнение теплообмена для воздуха

- граничное условие

Объемный коэффициент теплоотдачи в слое может быть рассчитан по эмпирической формуле:

Здесь 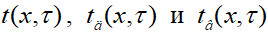 – температуры слоя, дыма и воздуха; x – координата, направленная по толщине слоя; τ – время; ρ и c – плотность и удельная теплоемкость материала насадки; d – диаметр частиц слоя; ε – порозность слоя;
– температуры слоя, дыма и воздуха; x – координата, направленная по толщине слоя; τ – время; ρ и c – плотность и удельная теплоемкость материала насадки; d – диаметр частиц слоя; ε – порозность слоя; 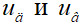 – скорости дыма и воздуха на свободное сечении насадки; cд и св – теплоёмкости дыма и воздуха; tд0 и tв0 – температуры дыма и воздуха на входе в насадку;
– скорости дыма и воздуха на свободное сечении насадки; cд и св – теплоёмкости дыма и воздуха; tд0 и tв0 – температуры дыма и воздуха на входе в насадку; 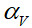 - объёмный коэффициент теплоотдачи; T – температура слоя, К.
- объёмный коэффициент теплоотдачи; T – температура слоя, К.
Основными показателями тепловой работы теплообменника являются температура подогрева холодного теплоносителя (воздуха) и значение коэффициента регенерации тепла, который может быть рассчитан по формуле:

Коэффициент регенерации показывает, какая доля тепла, поступившего в теплообменник с горячим теплоносителем, передается холодному теплоносителю. Чем ближе значение коэффициента регенерации к 1, тем эффективнее работает теплообменник.
Для решения поставленной задачи используем метод конечных разностей. В расчетной области вводим узловую сетку:
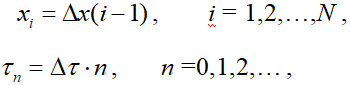
где 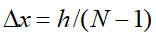 – шаг сетки по координате х;
– шаг сетки по координате х; 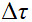 – шаг по времени; N– число узлов по координате х. Переходим к сеточным функциям
– шаг по времени; N– число узлов по координате х. Переходим к сеточным функциям 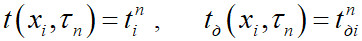 и
и 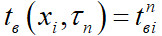 и дискретизируем задачу, применяя неявную разностную схему:
и дискретизируем задачу, применяя неявную разностную схему:
- для дымового цикла
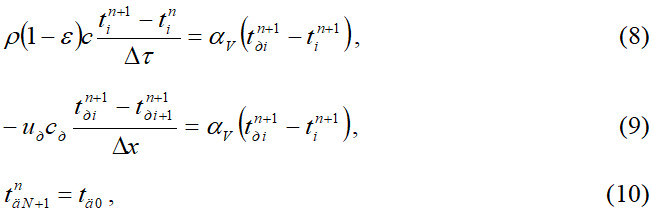
- для воздушного цикла
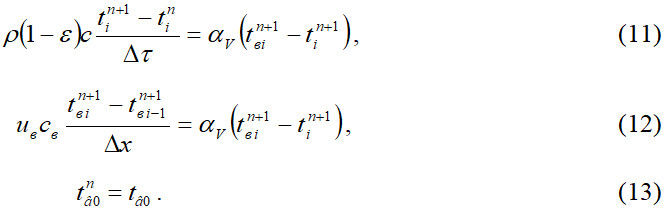
Для решения системы уравнений (8)–(13) для каждого значения n+1 применяем маршевый метод в направлении движения теплоносителя. Выражения (8) и (9) представим в виде системы из двух линейных алгебраических уравнений:

где коэффициенты при неизвестных определяются по следующим формулам:
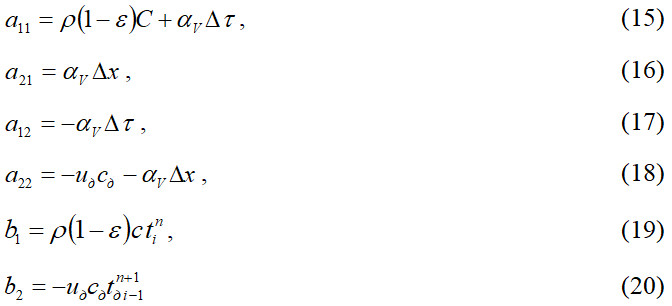
Решение системы уравнений (14) имеет вид:

Аналогичным образом получаются расчетные формулы для нахождения температур воздуха и насадки в узлах сетки для холодного периода.
Расчет начинается для горячего периода и выполняется в течение заданной длительности tп. Находятся температуры горячего теплоносителя и насадки в узлах сетки. Затем происходит изменение типа теплоносителя и направления его движения через насадку на противоположное. После этого расчет продолжается в течение времени tп и определяются температуры холодного теплоносителя и насадки в узлах сетки. После завершения моделирования одного цикла работы насадки аналогичным образом рассчитывается изменение ее температурного состояния в следующем цикле и т.д. до установления квазистационарного состояния.
Разработанная математическая модель позволяет:
- выполнить расчет разогрева насадки до наступления квазистационарного теплового состояния для заданных исходных данных;
- исследовать влияние высоты насадки на температуру подогрева воздуха и коэффициент регенерации тепла;
- исследовать влияние длительности горячего и холодного периодов на температуру подогрева воздуха;
- исследовать влияние отношения водяных чисел дыма и воздуха на температуру подогрева воздуха и коэффициент регенерации.

