Чемерис Ольга Анатоліївна
доцент кафедри алгебри та геометрії, кандидат педагогічних наук
Житомирський державний університет імені Івана Франка
Україна, місто Житомир
У різних розділах геометрії одне й те саме поняття означається по-різному, оскільки відрізняються основні методи цих розділів (координатний – в аналітичній геометрії, центрального проектування – в проективній, диференціального та інтегрального числення – в диференціальній геометрії тощо) [1]. Наприклад, означення трикутника в шкільній планіметрії таке: це фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки [2, с. 10]. У проективній геометрії ці точки з формулювання попарно належать прямим [3, с. 167]. Щодо означення чотирикутника, то маємо ще більше відмінностей у трактуванні поняття: це плоска фігура, яка складається з чотирьох точок, жодні три з яких не належать одній прямій, і шести прямих, які належать цим точкам попарно [3, с. 168].
Але розбіжність означення одного й того самого поняття у певних розділах геометрії накладає свої способи описання його характеристик та розв’язування практичних задач.
Розглянемо класичну задачу диференціальної геометрії щодо відшукання омбілічних точок. У диференціальній геометрії точка називається омбілічною, якщо в ній індикатриса Дюпена є колом [4, с. 134]. Звідси випливає І спосіб знаходження омбілічних точок, а саме, через дослідження квадратного рівняння деякої центральної кривої другого порядку:
ІІ спосіб знаходження омбілічних точок полягає в тому, що в них кривина 
не залежить від вибору напрямів 
, тому коефіцієнти першої та другої квадратичних форм пропорційні: 
[4, с. 134-135].
У курсі аналітичної геометрії з омбілічними точками ми зустрічаємось при вивченні питання про колові перерізи поверхонь другого порядку. Колові перерізи мають: 1) усі поверхні обертання; 2) поверхні другого порядку, рівняння яких можна подати в такому вигляді: 
, де 
– лінійні вирази відносно 
(мають дві серії колових перерізів) [5, с. 229].
Коли поверхня другого порядку замкнена, то серед площин, паралельних площинам колових перерізів, є такі, що зовсім її не перетинають, а також такі, що дотикаються до неї, або, як кажуть, перетинають її по колах нульового радіуса. Точки дотику цих площин з поверхнею називають точками закруглення, або омбілічними точками поверхні. Омбілічні точки поверхні обертання є точками перетину поверхні обертання з віссю обертання [5, с. 230].
Задача 5 з посібника [5, с. 232] про знаходження омбілічних точок еліпсоїда була розв’язана раніше [6, с. 161-165]. Опишемо розв’язання подібної задачі для знаходження точок заокруглення для еліптичного параболоїда 
.
Розв’язання.
Перейдемо в рівнянні еліптичного параболоїда до параметричної форми. Можна прийняти за параметри координати 
, тоді в координатно-параметричній формі рівняння поверхні набудуть вигляду:
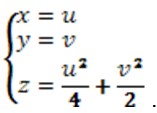
Обчислимо частинні похідні першого порядку для знаходження коефіцієнтів першої квадратичної форми:
.
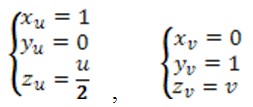Отже, 
Обчислимо частинні похідні другого порядку:
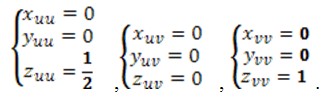
Тоді коефіцієнти другої квадратичної форми:
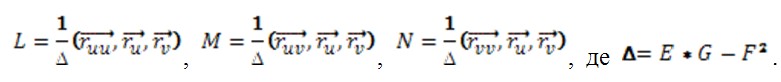Тепер: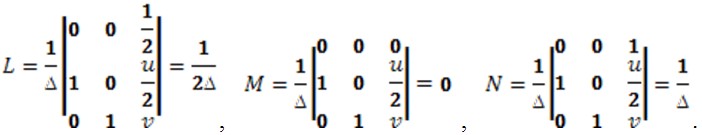 
Підставимо знайдені вирази для коефіцієнтів квадратичних форм в умову омбілічних точок 
: . Розв’язавши дану систему, маємо 
. Остаточно, маємо 
, або висновок: заданий еліптичний параболоїд має дві омбілічні точки: та 
.
В аналітичній геометрії ця задача на знаходження омбілічних точок для поверхонь другого порядку розв’язується швидше. Зробимо наступні перетворення з рівнянням еліптичного параболоїда: 
, 
.
Отже, площини 
та 
перетинають еліптичний параболоїд по колах. Взагалі дана поверхня має дві точки заокруглення [5, c. 231]. Знайдемо їх як точки дотику дотичних площин, паралельних заданим. З рівняння поверхні вектор нормалі дотичної площини має координати: 
Вектори нормалей площин, що є коловими перерізами, мають координати.
Площини – паралельні, тому вектори нормалей колінеарні, тобто їх координати пропорційні:
Тоді маємо 
. Підставимо це в рівняння поверхні і матимемо дві омбілічні точки: та 
.
Уміння студентом старших курсів означати поняття з боку різних розділів однієї науки чи певних дисциплін є важливим компонентом фахової підготовки і свідчить про його компетентність.
Література:
1. Явище – поняття – визначення – термін [Електронний ресурс]. – Режим доступу до сторінки: http://stud.com.ua/30973/pravo/yavische_ponyattya_viznachennya_termin.
2. Бурда М.І. Геометрія: підручник для 7 класу загальноосвітніх навчальних закладів / Бурда М.І., Тарасенкова Н.А. - К. : Зодіак-ЕКО, 2007. - 208 с.
3. Боровик В.Н. Курс вищої геометрії: Навчальний посібник / [В.Н. Боровик, В.П. Яковець] – Суми: ВТД «Університетська книга», 2004. – 464 с.
4. Кованцов М.І. Диференціальна геометрія / Микола Іванович Кованцов. – К.: Вища школа, 1973. – 276 с.
5. Аналітична геометрія / [Білоусова В. П., Ільїн І. Г., Сергунова О. П., Котлова В. М.]. – К.: Вища школа, 1973. – 328 с.
6. Чемерис О.А. Науковий пошук молодих дослідників: збірник наукових праць студентів, магістрантів та викладачів / за ред. доц. О.М. Королюк. – Житомир: Вид-во ЖДУ ім. І. Франка. – Вип. 9. – С. 161-165.
