На головну

Недашківська Надія Іванівна 

к.т.н, доц., ННК «ІПСА» НТУУ «КПІ» ,Україна, м. Київ

Головатюк В.О 

студент, ННК «ІПСА» НТУУ «КПІ», Україна, м. Київ

  У статті висвітлено результати дослідження моделей парних порівнянь для методу аналізу ієрархій із застосуванням інтервальних значень оцінок експертів. Проведено аналіз роботи моделей на прикладі матриць парних порівнянь різного рівня узгодженості.

  Метод аналізу ієрархій (МАІ) було запропоновано в кінці 1970-х років американським математиком Т. Салаті. Метод полягає у декомпозиції проблеми на більш прості складові і поетапному встановленні пріоритетів оцінюваних компонент з використанням парних порівнянь.  МАІ включає в себе процедуру синтезу множинних суджень, отримання пріоритетності критеріїв і знаходження альтернативних рішень.[1]

  В багатьох випадках модель відношення переваги, якою користується Особа що приймає рішення (ОПР) невизначена та нечітка і досить складно отримати чітке числове вираження порівняльних суджень експерта. Для Вирішення цієї задачі використовують модифіковані методи аналізу ієрархій ММАІ. Однією з найбільш поширених модифікацій є заміна точкових оцінок пріоритетів інтервальними значеннями. 

  Розглянемо моделі парних порівнянь, що обчислюють ваги на підставі інтервальних оцінок експерта. Вважається, що надання оцінок в нечіткому вигляді зменшує навантаження на експерта, враховуючи, що  замість точкових оцінок експерт дає більш зручні для нього і, одночасно, більш відповідні реальності лінгвістичні оцінки типу «приблизно дорівнює x», «між величиною x і y». Зокрема, розроблено досить багато моделей для обчислення ваг елементів прийняття рішень на підставі інтервальних МПП (ІМПП).  . [2]

  У даній роботі досліджуються GPM, LUAM і Адитивна моделі [3], результатом роботи яких є інтервальні ваги альтернатив рішень.

  Для автоматизації процесу дослідження моделей формується чітка матриця парних порівнянь, яка поступово модифікується шляхом імовірнісного відхилення значень її елементів.

  Під час її формування, враховується що така матриця має водночас бути діагональною та зворотньо-симетричною, а також має враховуватись умова транзитивності. [2].

  Наступним кроком, є приведення оцінок сильно узгодженої матриці парних порівнянь до шкали запропонованої Т. Сааті, шляхом округлення нецілочисельних значень парних порівнянь, значення яких, більше за одиницю, і відповідний перерахунок, обернених до них елементів.

  Формування слабко (порядково) узгоджених МПП, як чітких так і інтервальних, відбувається з додаванням шумів, і приведенням їх до шкали запропонованої Т. Сааті. 

  Зашумлення матриці парних порівнянь виконується з урахуванням величини значень елементів.

  Елементи зашумленої матриці знаходяться з співвідношення:

  Де  – випадковий коефіцієнт, отриманий відповідно до заданого користувачем розподілу. В даному дослідженні використовується нормальний розподіл, для якого математичне сподівання дорівнює нулю, а середньоквадратичне відхилення σ ≤ 0,15.

  За допомогою розробленої системи моделювання було проведено ряд дослідів, спрямованих на дослідження запропонованих моделей знаходження локальних ваг альтернатив.

  Розглянемо приклад, для матриць марних порівнянь та різного рівня узгодженості розмірності n=3.

  В якості опорного рішення будемо використовувати частковий випадок сильно узгоджені чіткі матриці парних порівнянь A, та порядково узгоджені матриці А1 заповнені за шкалою Сааті приведені на рисунку 1.

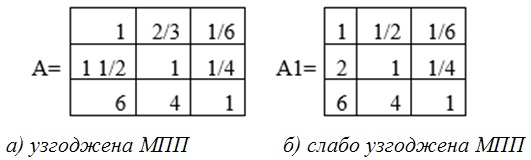
Рисунок 1 Чіткі матриці парних порівнянь

  Для розрахунку локальних ваг елементів застосовуються методи головного власного вектору (EM). Проаналізувавши результати (таблиця 1), ми бачимо, що обидві матриці призвели до однакового ранжування. Для визначення рівня узгодженості в методі ЕМ використовується відношення узгодженості  , низькі значення якого свідчать, про гарну узгодженість матриць. Для повністю узгодженої матриці А цей показник дорівнює 0

Таблиця 1 Ваги отримані на основі МПП А і А1 

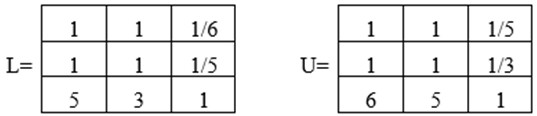
  Останнім етапом розглянемо слабко неузгоджені інтервальні матриці парних порівнянь (рисунок. 4), елементи якої окрім викидів, допустимо неузгоджені. На основі цієї матриці отримано наступні результати (таблиця 4)

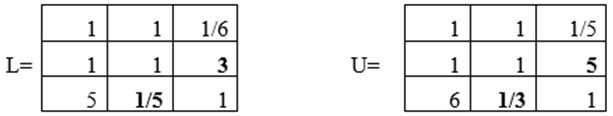
Рисунок 4 Слабко згоджена ІМПП (L, U)

Таблиця 4 Ваги отримані на основі слабко неузгодженої ІМПП

  Майже всі розглянуті моделі привели до чітких однаковим ваг в разі повністю узгодженої МПС, лише результат Адитивної моделі призвів до інших рангів. У випадку, якщо ІМПС неузгоджена, ваги за різними методами будуть відрізнятися, однак у багатьох випадках ці ваги задають однакову ранжування альтернатив рішень. Так, для слабо узгодженої ІМПС ранжування за всіма методами  збігається з ранжируванням за традиційним методом головного власного вектора EM.  Для таких МПС в основному виконується властивість слабкої збереження порядку. У найбільш неузгоджену випадку, коли в ІМПС є нетранзитивні елементи (цикл), ранжирування, отримані різними моделями, в основному, відрізняються між собою.

Список літератури

1.Саати, Т. Л. Принятие решений. Метод анализа иерархий [Текст] / Т. Л. Саати. – М.: Радио и связь, 1993. – 320c.

2.Панкратова Н.Д., Недашківська Н.І. Метод і моделі аналізу ієрархій. Теорія. Застосування навч. посіб. – К.: НТУУ «КПІ» 2010. -372 с.

3.Zhou-Jing Wang ,Kevin W. Li Goal programming approaches to deriving interval weights based on interval fuzzy preference relations //Information Sciences. -2012 193, P. 180–198